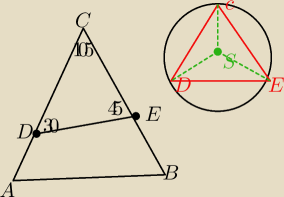
 dany jest trójkąt abc o bokach AC=6 i BC=3*√2. Na boku AC tego trójkąta obrano punkt D a na
boku BC punkt E, tak że kąt CDE=30 i kąt DEC=45 oraz promień okręgu opisanego na trójkącie CDE
jest równy 2*√2. Wykaż że odcinki DE i AB są równoległe.
Ale że tak powiem na rysunku mój pomysł się kończy. Ano i jeszcze bym zaproponował tutaj tw.
odwrotne do talesa, ale już wyobraźnia ma nie podpowiada mi co dalej... kąt środkowy 210, ale
który to?
dany jest trójkąt abc o bokach AC=6 i BC=3*√2. Na boku AC tego trójkąta obrano punkt D a na
boku BC punkt E, tak że kąt CDE=30 i kąt DEC=45 oraz promień okręgu opisanego na trójkącie CDE
jest równy 2*√2. Wykaż że odcinki DE i AB są równoległe.
Ale że tak powiem na rysunku mój pomysł się kończy. Ano i jeszcze bym zaproponował tutaj tw.
odwrotne do talesa, ale już wyobraźnia ma nie podpowiada mi co dalej... kąt środkowy 210, ale
który to?
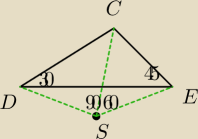 Trochę źle narysowałeś− trójkąt DEC jest rozwartokątny
Kąt DEC jest wpisany oparty na łuku DC, a kąt DSC to środkowy oparty na tym samym łuku
Kąt CSE to kąt środkowy oparty na tym samym łuku, co wpisany CDE.
r=2√2, więc
|DC|=2√2*√2=4
|CE|=r=2√2
I masz:
Trochę źle narysowałeś− trójkąt DEC jest rozwartokątny
Kąt DEC jest wpisany oparty na łuku DC, a kąt DSC to środkowy oparty na tym samym łuku
Kąt CSE to kąt środkowy oparty na tym samym łuku, co wpisany CDE.
r=2√2, więc
|DC|=2√2*√2=4
|CE|=r=2√2
I masz:
| |CD| | 4 | 2 | |||
= | = | ||||
| |AC| | 6 | 3 |
| |CE| | 2√2 | 2 | |||
= | = | ||||
| |BC| | 3√2 | 3 |
