Proszę o pomoc. Rozwiąż nierówność z wartością bezwzgledną
paulina3009:
a) ||x+1|−x|≤2
b) |x−2|−|x+3|≥1+x
29 sty 20:46
Eve:
a) Ix+1I−x≤2 lub Ix+1I−x≥2
29 sty 20:48
paulina3009: to znaczy ja jak do tej pory robilam przyklad a w ten sposob:
−2≤|x+1|−x≤2
−2≤x+1−x≤2
−2≤1≤2
no ale skoro tak wychodzi to powinna być chyba odpowiedz x∊R
no a w przypadku x=−10 nierówność już nie zachodzi
więc coś mam źle ale nie wiem w którym miejscu
29 sty 20:59
paulina3009: i dlatego proszę o pomoc
29 sty 20:59
Eve: no tak, bo Ix+1I może być równa −x−1
29 sty 21:01
paulina3009: no ale jesli |x+1|=−x−1 to wtedy −x powinno sie zmienic na +x czy źle myślę?
|−x−1|+x|≤2
29 sty 21:04
dawek: nie ma być przypadkiem w przykładzie a spójnik " i " a nie lub

29 sty 21:06
paulina3009: sorki za blad ||−x−1|+x|≤2
29 sty 21:07
paulina3009: no spojnik i to na pewno ale co dalej?
29 sty 21:07
dawek: rozbijasz na 2 równania i masz
|−x−1|−x<2 i |−x−1|−x>2
−x−1<x+2 i −x−1>x+2 −x−1>2+x LUB −x−1>2+x
tam ma być większe i mniejsze bądź równe. Ja bym tak to zrobił

29 sty 21:12
paulina3009: to znaczy tak chyba nie powinno byc bo jedna z wlasnosci mowi ze
|x|<a⇔−a<X<a
no ale tak jak pisalam zgodnie z ta wlasnoscia mi nie wychodzi
bo przy x∊R w przypadku x=−10 nierownosc jest falszywa
29 sty 21:16
Eve:
w a) mi wyszedł przedział [−1/2;1/2] tak?
29 sty 21:20
paulina3009: to znaczy ja niestety nie mam do tego odpowiedzi bo nauczyciel dal nam zadanka na kserowkach
29 sty 21:22
paulina3009: a ze mi nie wychodzi to dlatego pomyslalam ze ktos moglby mi pomoc
sprawdzalam ze przy x=−5 nierownosc zachodzi
wiec chyba to takze nie jest odpowiedz
29 sty 21:23
paulina3009: nie przepraszam przy x=−5 nie zachodzi
a jak to zrobilas Eve ?
29 sty 21:29
Eve: i dlatego ma być lub a nie i

29 sty 21:32
Eve: Ix+1I−x≤2
x+1−x≤2 zachodzi dla każdej liczby
−x−1−x≥2
−2x≥1
lub
Ix+1I−x≥−2
x+1−x≥2 zachodzi dle każdej liczby
−x−1−x≥−2
−2x≥−1
| | 1 | | 1 | |
zaznacz na osi i zobaczysz, że x∊[−∞, − |
| ]∪[ |
| ,∞] |
| | 2 | | 2 | |
29 sty 21:36
paulina3009: a tam nie powinno byc ze −x−1−x≥2 −2x≥3 ?
29 sty 21:42
Mila:
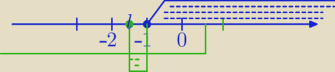
1)
||x+1|−x|≤2⇔
|x+1|−x≥−2 i |x+1|−x≤2
|x+1|=x+1 dla x≥−1
wtedy mamy :
x+1−x≥−2 i x+1−x≤2
1≥−2 i 1≤2 nierówności prawdziwe niezależnie od wyboru x z przedziału <−1,
∞)
lub
2) |x+1|=−x−1 dla x<−1 wtedy mamy nierówności:
−x−1−x≥−2 i −x−1−x≤2
−2x≥−1 i −2x≤3
| | 1 | | 3 | | 3 | |
x≤ |
| i x≥− |
| i x<−1⇔x∊<− |
| ,−1) |
| | 2 | | 2 | | 2 | |
Z (1) , (2)
29 sty 21:52
paulina3009: wieeelkie dzieki Mila
29 sty 22:54
Mila:
29 sty 23:39



 1)
||x+1|−x|≤2⇔
|x+1|−x≥−2 i |x+1|−x≤2
|x+1|=x+1 dla x≥−1
wtedy mamy :
x+1−x≥−2 i x+1−x≤2
1≥−2 i 1≤2 nierówności prawdziwe niezależnie od wyboru x z przedziału <−1,∞)
lub
2) |x+1|=−x−1 dla x<−1 wtedy mamy nierówności:
−x−1−x≥−2 i −x−1−x≤2
−2x≥−1 i −2x≤3
1)
||x+1|−x|≤2⇔
|x+1|−x≥−2 i |x+1|−x≤2
|x+1|=x+1 dla x≥−1
wtedy mamy :
x+1−x≥−2 i x+1−x≤2
1≥−2 i 1≤2 nierówności prawdziwe niezależnie od wyboru x z przedziału <−1,∞)
lub
2) |x+1|=−x−1 dla x<−1 wtedy mamy nierówności:
−x−1−x≥−2 i −x−1−x≤2
−2x≥−1 i −2x≤3