pole czworokąta ABCD o wierzchołkach
rombek: pole czworokąta ABCD, gdzie A(−5,−2), B(4,1), C(−2,8), D(−6,3) jest równe: (odp. 53)
moje rozwiązanie:
czworokąt ABCD "rozbić" na dwa trójkąty; obliczyć pola trójkątów i je zsumować. zrobiłem to, a
ciągle mi nie wychodzi, już nie wytrzymuję, proszę o wytknięcie błędu:
P
ABC+P
DCA=P
ABCD
| | 1 | | 1 | | 99 | |
PABC: |
| |(4+5)(8+5)−(1+5)(−2+5)|= |
| |117−18|= |
| |
| | 2 | | 2 | | 2 | |
| | 1 | | 1 | | 34 | |
PADC: |
| |(−6+5)(8+2)−(3+5)(−2+5)|= |
| |−10−24|= |
| |
| | 2 | | 2 | | 2 | |
| | 133 | |
co po zsumowaniu daje |
| = 66,5 |
| | 2 | |
już nie mogę, podstawiam chyba 5 raz pod ten wzór i wychodzi mi ciągle co innego, może ktoś
wytknąć mi błędy?
29 sty 17:17
rombek: już widzę pierwszy błąd − trzeci nawias w polu ABC powinien być (1+2), co zmieni wynik i da:
PABC=54 i to już daje większe pole niż w odpowiedzi, nie wiem, co robić.. jakaś inna metoda
wyznaczenia tego pola?
29 sty 17:21
Mila:
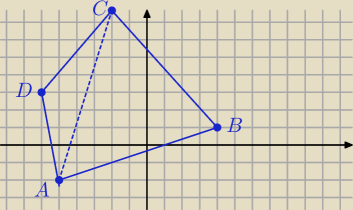
Liczę współrzędne wektorów i wyznaczniki:
AC
→=[3,10]
AB
→=[9,3]
3 10
9 3
| | 1 | | 81 | |
PΔABC= |
| |3*3−9*10|= |
| |
| | 2 | | 2 | |
AD
→=[−1,5]
3 10
−1 5
| | 1 | | 25 | |
PΔACD= |
| *|3*5−10*(−1)|= |
| |
| | 2 | | 2 | |
29 sty 17:28
rombek: o, zawsze inna metoda niż tamta.
dziękuję Mila

29 sty 17:32
Tadeusz:
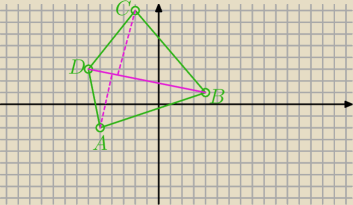
29 sty 17:45
rombek: Tadeusz, sugerujesz, żeby obliczyć |BD|, obliczyć wysokość czyli odległość od C do punktu
przecięcia się prostej prostopadłej przechodzącej przez C do prostej przechodzącej przez BD?
oraz to samo z drugim trójkątem, dobrze rozumiem?
29 sty 17:48
rombek: poprawiam się: wysokość czyli odległość C od prostej przechodzącej przez B, D.
29 sty 17:51
 Liczę współrzędne wektorów i wyznaczniki:
AC→=[3,10]
AB→=[9,3]
3 10
9 3
Liczę współrzędne wektorów i wyznaczniki:
AC→=[3,10]
AB→=[9,3]
3 10
9 3

