 Witam,
Mam problem z zadaniem z stereometrii, a dokładniej z poddziału "Przekroje ostrosłupów". Na
pewno nie jest ono ciężkie, bo jak powszechnie wiadomo podręcznik "Nowej Ery" trudnych zadań
nie ma, ale mimo to, nie mogę sobie z nim poradzić. Po narysowaniu, wiem, że da się to jakoś
obliczyć, ale jak?
Oto treść:
Ostrosłup prawidłowy czworokątny o krawędzi podstawy a przecięto płaszczyzną przechodzącą przez
jego wierzchołek i środki sąsiednich krawędzi podstawy. Płaszczyzna ta tworzy z podstawą kąt
α. Wyznacz pole otrzymanego przekroju oraz objętość tego ostrosłupa.
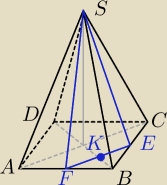
Taki mam rysunek.
W swoim rozwiązaniu doszedłem do tego, że
Witam,
Mam problem z zadaniem z stereometrii, a dokładniej z poddziału "Przekroje ostrosłupów". Na
pewno nie jest ono ciężkie, bo jak powszechnie wiadomo podręcznik "Nowej Ery" trudnych zadań
nie ma, ale mimo to, nie mogę sobie z nim poradzić. Po narysowaniu, wiem, że da się to jakoś
obliczyć, ale jak?
Oto treść:
Ostrosłup prawidłowy czworokątny o krawędzi podstawy a przecięto płaszczyzną przechodzącą przez
jego wierzchołek i środki sąsiednich krawędzi podstawy. Płaszczyzna ta tworzy z podstawą kąt
α. Wyznacz pole otrzymanego przekroju oraz objętość tego ostrosłupa.
Taki mam rysunek.
W swoim rozwiązaniu doszedłem do tego, że
| a | ||
|FE|= | ||
| 2 |
| 3a√2 | ||
|DK|= | ||
| 4 |

| 1 | ||
|FE|= | |AC| | |
| 2 |
| OK | ||
cosα= | ||
| SK |
| 1 | |
a√2=|SK|*cosα | |
| 4 |
| a√2 | ||
|SK|= | ||
| 4cosα |
| H | ||
tgα= | ||
| 14a√2 |
| 1 | a√2 | a√2 | a2 | |||||
Pprzekrój= | * | * | = | |||||
| 2 | 2 | 4cosα | 8cosα |
| 1 | a√2tgα | a3√2tgα | ||||
Vostrosłup= | *a2* | = | ||||
| 3 | 4 | 12 |


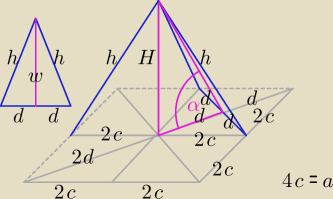 d = c√2, H = d*tgα ⇒ H = c√2tgα, h = √H2 + (2c)2 = ..., w = √h2 − d2 = ...
d = c√2, H = d*tgα ⇒ H = c√2tgα, h = √H2 + (2c)2 = ..., w = √h2 − d2 = ...
| 1 | ||
Objętość: V = | *(4c)2*H | |
| 3 |

