trojkąt Mariusz: PROSZĘ O POMOC w trójkącie suma dwóch boków jest równa 6, a kąt między tymi bokami jest równy 120 stopni. Oblicz jaki najmniejszy wymiar może mieć bok leżący naprzeciwko tego kąta

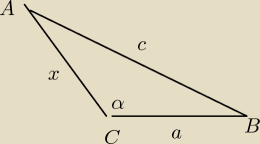
AS: Dane: a + x = 6 , α = 120^o Z tw. cosinusów: c² = a² + x² − 2*a*x*cos(α) ; cos(α) = cos(120^o) = −1/2 c² = (6 − x)² + x² − 2*(6 − x)*x*(−1/2) c² = 36 − 12*x + x² + x² + 6*x − x² c² = x² − 6*x + 36 Ponieważ interesują mnie wartości ekstremalne,badam kwadrat boku c

	−b		6
xw =		=		= 3
	2*a		2*1

a = 6 − xw = 6 − 3 = 3 Boki trójkąta a = 3 , x = 3 Bok c² = 3² − 6*3 + 36 = 9 − 18 + 36 = 27 c = √27 = √9*3 = 3*√3 Odp. Najmniejszy wymiar szukanego boku wynosi 3*√3