TEST X Blue: zad.11 Udowodnij, że łącząc środki boków trapezu równoramiennego otrzymamy romb.

	1		1		1		1
zad. 18 Rozważmy funkcję y =		+		+		+		.
	x		x+1		x+2		x+3

c) Określ liczbę rozwiązań równania f(x) = 0 d) Podaj liczbę rozwiązań równania f(x) =m w zależności od parametru m. http://i57.tinypic.com/vec29h.jpg Proszę o pomoc z tymi zadankami, coś tam napisałam w 11, ale pewnie źle to jest

Kacper: W 11 dlaczego są równoramienne? To zadanie jest standardowe na użycie twierdzenia o odcinku łączącym środki dwóch dowolnych boków w trójkącie. Spróbuj w ten sposób rozwiązać

Kacper: W 18 nie umiesz rozwiązać takiego równania?

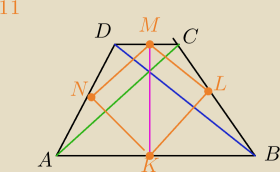
Mila: 11) |AC|=|BD| − przekątne w trapezie równoramiennym są równe

	1
KL||AC i |KL|=		|AC| jako odcinek łącący środki boków ΔACB
	2

	1
MN||AC i |MN|=		|AC| jako odcinek łącący środki boków ΔACD
	2

	1
ML||BD i |ML|=		|BD|
	2

	1
KN|| BD i |KN|=		|BD|
	2

⇔ |ML|=|KN|=|KL|=|MN|⇔ Czworokąt KLMN jest rombem.

Blue: Dziękuję Mila Kacper próbowałam to 18 rozwiązać, ale nie wychodzi wielomian 3−go stopnia i jakoś nie mogę wpaść na pierwiastek

Mila: 1) D 2) Masz określić liczbę rozwiązań. ( Nie pytają jakie to są rozwiązania) Pochodna.

Mila: 3) Granice lewostronne i prawostronne w punktach nieciągłości. 4) Granica w ∞,−∞.

Blue: Pochodna jest ujemna dla x ∊R\{−3,−2,−1,0} , czyli funkcja jest malejąca.... lim = 0 x−> ∞ lim= 0 x−>− ∞ lim = ∞ x−>−3⁺ lim= − ∞ x−>−3⁻ lim = ∞ x−>−2⁺ lim= − ∞ x−>−2⁻ lim= ∞ x−>−1⁺ lim= − ∞ x−>−1⁻ Czyli są trzy rozwiązania, bo są trzy nieskończoności? Możesz Mila sprawdzić, czy to jest dobrze? i ile będzie miała granica w punkcie 0? też 0

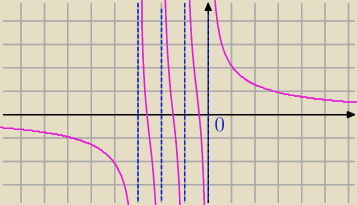
Mila: f'(x)<0 dla x∊D⇔f(x) jest malejąca przedziałami. ( Nie możesz napisać tylko, że "jest malejąca") 1) x∊(−∞,−3) f(x)<0 i lim_x→−∞ f(x)=0 lim_x→−3−=−∞ brak miejsca zerowego w tym przedziale. 2)x∊(−3,−2) f(x) jest ciągła w tym przedziale lim_x→−3+f(x)=∞ lim_x→−2−f(x)=−∞⇔istnieje x₀∊(−3,−2), że f(x₀)=0 3) podobnie w przedziale (−2,−1) oraz (−1,0)

Blue: ok, dziękuję Ci bardzo Milu