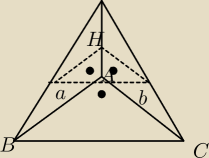
Stereometria Pawel: Podstawą ostrosłupa o wys. H jest trójkąt prostokątny ABC o przyprostokątnych |AB|=a i |AC|=b. Krawędź boczna wychodząca z wierzchołka A jest prostopadła do podstawy. Ostrosłup ten podzielono płaszczyzną równolełą do podstawy na dwie bryły o równych objętościach. Oblicz pole pow. tej bryły, która nie jest ostrosłupem. Bardzo proszę o pomoc w tym zadaniu, nigdzie nie mogę znaleźć rozwiązania ani wskazówki co robić.

Krystek:

	1
Vc=		a*b*H i dalej myśl
	2

Pawel:

	1
a nie przypadkiem V=		a*b*H ?
	3

Krystek: Oczywiście!

Krystek: Byłam na wagarach jak uczyli!

Pawel: tylko co dalej

Pawel:

	1
skala podobieństwa górnego ostrosłupa do całości k=
	3√2

irena_1: Odcięty ostrosłup jest podobny do wyjściowego. Stosunek objętości podobnych brył jest równy sześcianowi skali podobieństwa, czyli skala podobieństwa odciętego (małego) ostrosłupa do ostrosłupa wyjściowego jest równa

	1		3√4
k=3√		=
	2		2

Trzeba policzyć powierzchnię boczną dużego ostrosłupa. Od niej odjąć powierzchnię boczną małego ostrosłupa (powierzchnia boczna małego jest równa k²* powierzchnia boczna ostrosłupa wyjściowego). Do pola powierzchni wchodzi też podstawa dużego i podstawa małego ostrosłupa (też stanowi k² pola podstawy wyjściowego ostrosłupa)

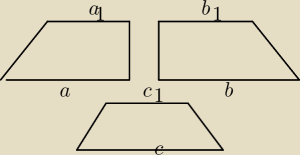
Krystek: Sciany boczne i licz

Pawel: dzięki