| 2P | ||
liczyłem z wzoru R = | ale nie wyszło  | |
| a+b+c |
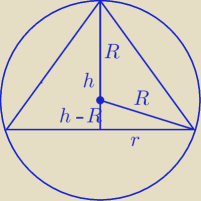 Załóżmy, że h > R
(h − R)2 + r2 = R2
r2 = R2 − (h − R)2
r = √R2 − (h − R)2
Załóżmy, że h > R
(h − R)2 + r2 = R2
r2 = R2 − (h − R)2
r = √R2 − (h − R)2
| 1 | 1 | |||
V = | πr2h = | π*(R2 − (h − R)2)h | ||
| 3 | 3 |
 A sory, źle przeczytałem,
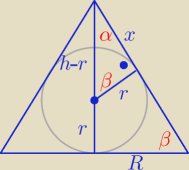
Z twierdzenia Pitagorasa: r2 + x2 = (h − r)2 ⇒ x = √(h − r)2 − r2
Z podobieństwa trójkątów (mam nadzieję, że widać jakich)
A sory, źle przeczytałem,
Z twierdzenia Pitagorasa: r2 + x2 = (h − r)2 ⇒ x = √(h − r)2 − r2
Z podobieństwa trójkątów (mam nadzieję, że widać jakich)
| R | h | hr | |||
= | ⇒ R = | ||||
| r | x | √(h − r)2 − r2 |
| 1 | h2r2 | |||
V = | π | * h | ||
| 3 | (h − r)2 − r2 |
