proszę o pomoc
wioletkaaa1995: napisz równanie parametryczne prostej przechodzącej przez punkt P=(1,2,3)
i równoległej do płaszczyzn π1=x+y+z=0 i π2=x−y+z−7=0.
27 sty 20:37
Godzio:
Wektory normalne płaszczyzn:
N
1 = (1,1,1)
N
2 = (1,−1,1)
skoro prosta jest równoległa do obu to musi być prostopadła do wektorów normalnych stąd
wyliczamy jej wektor kierunkowy K
K = (1,1,1) x (1,−1,1) = (2,0,−2)
Dodatkowo wiemy, że przechodzi przez punkt P(1,2,3) więc zapisujemy równanie prostej k.
| | ⎧ | x = 1 + 2t | |
| k = | ⎨ | y = 2 |
|
| | ⎩ | z = 3 − 2t | |
27 sty 20:46
wioletkaaa1995: dziękuję bardzo

27 sty 21:17
wioletkaaa1995: a to zadanie?
napisz równanie parametryczne prostej zawartej w płaszczyźnie π=2x−y+z+3=0
i prostopadłej do prostej l: x+43= y−3−1 = z+23.
27 sty 21:23
Godzio:
Tym razem nie będzie tak łatwo, zrobimy to razem

Napisz mi ...
Wektor normalny płaszczyzny: N = ...
Wektor kierunkowy prostej: K = ...
Jak w stosunku do tych wektorów musi leżeć wektor kierunkowy K
1 szukanej prostej?
27 sty 21:27
wioletkaaa1995: n=(2,−1,1)
k=(3,−1,3)
27 sty 21:29
wioletkaaa1995: a co do położenia wektora to nie mam bladego pojęcia

jakoś nie umiem sobie tego wyobrazić...
27 sty 21:31
Godzio:
Super, to jeszcze odpowiedz na ostatnie pytanie

27 sty 21:31
Godzio:
1. Jak leży w stosunku do płaszczyzny jej wektor normalny?
2. Skoro proste są prostopadłe, to ich wektory kierunkowe są do siebie ... ?
27 sty 21:31
wioletkaaa1995: a może musi być prostopadły

27 sty 21:32
wioletkaaa1995: 1. prostopadle
2.prostopadłe

27 sty 21:32
wioletkaaa1995: wiem że gdy dwa wektory są prostopadłe to ich iloczyn skalarny jest równy 0...
ale nie wiem czy należy to tutaj wykorzystać...
27 sty 21:34
Godzio:
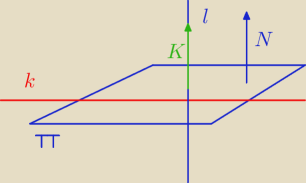 Uwaga
Uwaga K i N nie muszą być równoległe (tylko tak na rysunku wyszło, ale tak nie jest)
No właśnie, skoro wektor normalny jest prostopadły do płaszczyzny, to w jakim jest on stosunku
do prostej zawartej w tej płaszczyźnie?
27 sty 21:35
Godzio:
Co do skalarnego − ok, ale to się tu nie przyda

27 sty 21:35
wioletkaaa1995: też jest prostopadły
27 sty 21:36
Godzio:
No właśnie szukamy wektora kierunkowe prostej K1 prostopadłego do N i K. Jak znajduje się
wektor prostopadły jednocześnie do dwóch innych danych wektorów?
27 sty 21:38
wioletkaaa1995: nie mam pojęcia...
27 sty 21:38
Godzio:
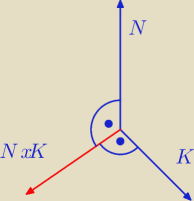
No to sobie zapisz, że wektor prostopadły do dwóch danych wektorów (nierównoległych) to iloczyn
wektorowy tychże wektorów.
Stąd mamy K
1 = N x K = (2, −1, 1) x (3, −1, 3)
Wiadomo jak się liczy taki iloczyn?
27 sty 21:41
wioletkaaa1995: tak wiadomo

27 sty 21:43
wioletkaaa1995: K1=(−2,−3,1)?
27 sty 21:45
Godzio: No to policz, mamy już wektor kierunkowy prostej, jak teraz zagwarantować, że będzie zawierała
się w płaszczyźnie? (wiemy już, że skoro jest prostopadła do wektora normalnego to jest
równoległa do płaszczyzny, ale my chcemy, żeby była w niej zawarta)
27 sty 21:46
Godzio: Tak.
27 sty 21:46
wioletkaaa1995: pomocy...
27 sty 21:49
Godzio:
Gdyby prosta przechodziła przez dowolny punkt płaszczyzny, to już będzie w niej zawarta?
Narysuj prostą równoległą do płaszczyzny przechodzącą przez dowolny jej punkt.
27 sty 21:51
wioletkaaa1995: tak wtedy prosta będzie w niej zawarta
27 sty 21:54
Godzio:
No to weź dowolny punkt (x,y,z), który spełnia równanie płaszczyzny.
Podam przykładowy, ale podaj mi inny proszę

2x−y+z+3=0 noto ja wezmę x = 0, y = 0, z = −3 i mam (0,0,−3) bo
2 * 0 − 0 − 3 + 3 = 0 = 0 (działa!)
Wiadomo jak powstaje równanie parametryczne prostej?
27 sty 21:56
wioletkaaa1995:

27 sty 21:57
wioletkaaa1995: tak wiadomo

inny taki punkt to np (1,2,−3)
27 sty 21:59
Godzio:
Super

No to masz koniec zadania, mam nadzieję, że już się trochę rozjaśniło!

27 sty 22:00
wioletkaaa1995: czyli l: x= 1−2t y=2−3t z=−3−t gdzie t ∊ℛ
27 sty 22:01
wioletkaaa1995: dziękuję

27 sty 22:01
Godzio:

27 sty 22:02

 Napisz mi ...
Wektor normalny płaszczyzny: N = ...
Wektor kierunkowy prostej: K = ...
Jak w stosunku do tych wektorów musi leżeć wektor kierunkowy K1 szukanej prostej?
Napisz mi ...
Wektor normalny płaszczyzny: N = ...
Wektor kierunkowy prostej: K = ...
Jak w stosunku do tych wektorów musi leżeć wektor kierunkowy K1 szukanej prostej?
 jakoś nie umiem sobie tego wyobrazić...
jakoś nie umiem sobie tego wyobrazić...



 Uwaga K i N nie muszą być równoległe (tylko tak na rysunku wyszło, ale tak nie jest)
No właśnie, skoro wektor normalny jest prostopadły do płaszczyzny, to w jakim jest on stosunku
do prostej zawartej w tej płaszczyźnie?
Uwaga K i N nie muszą być równoległe (tylko tak na rysunku wyszło, ale tak nie jest)
No właśnie, skoro wektor normalny jest prostopadły do płaszczyzny, to w jakim jest on stosunku
do prostej zawartej w tej płaszczyźnie?

 No to sobie zapisz, że wektor prostopadły do dwóch danych wektorów (nierównoległych) to iloczyn
wektorowy tychże wektorów.
Stąd mamy K1 = N x K = (2, −1, 1) x (3, −1, 3)
Wiadomo jak się liczy taki iloczyn?
No to sobie zapisz, że wektor prostopadły do dwóch danych wektorów (nierównoległych) to iloczyn
wektorowy tychże wektorów.
Stąd mamy K1 = N x K = (2, −1, 1) x (3, −1, 3)
Wiadomo jak się liczy taki iloczyn?

 2x−y+z+3=0 noto ja wezmę x = 0, y = 0, z = −3 i mam (0,0,−3) bo
2 * 0 − 0 − 3 + 3 = 0 = 0 (działa!)
Wiadomo jak powstaje równanie parametryczne prostej?
2x−y+z+3=0 noto ja wezmę x = 0, y = 0, z = −3 i mam (0,0,−3) bo
2 * 0 − 0 − 3 + 3 = 0 = 0 (działa!)
Wiadomo jak powstaje równanie parametryczne prostej?

 inny taki punkt to np (1,2,−3)
inny taki punkt to np (1,2,−3)
 No to masz koniec zadania, mam nadzieję, że już się trochę rozjaśniło!
No to masz koniec zadania, mam nadzieję, że już się trochę rozjaśniło! 

