Zadanie z równoległobokiem. glik: Równoległobok EFGH o obwodzie 16 jest obrazem równoległoboku ABCD w podobieństwie o skali 1/3. Oblicz długości boków równoległoboku EFGH, wiedząc, że stosunek wysokości równoległoboku ABCD wynosi 2/3.

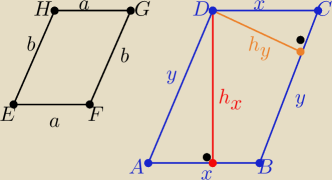
Eta: dla równoległoboku EFGH :

	1
2a+2b=16 ⇒ a+b=8 , skala podobieństwa k=
	3

to w równoległoboku ABCD : x+y=8*3 ⇒ x+y=24

	hx		2		y		2		2
i		=		⇒		=		⇒ y=		x
	hy		3		x		3		3

	2		72		48
to: x+y=24 ⇒ x+		x=24 ⇒ x=		i y=
	3		5		5

	1		72		24
zatem a= k*x=		*		=		i b=k*y= ...........
	3		5		5