analiza matematyczna w geometrii analitycznej orzech:

	1
wykaż że styczna do paraboli o równaniu y=		x2 −3x −2 poprowadzona w punkcie P o
	2

odciętej 2, ogranicza wraz z osiami układu współrzędnych trójkąt o polu równym 8. z polecenia wynika, że punkt P = (2, y), a styczna ma równanie: y=2a+b, ale co więcej? myślałem o czymś takim: f'(x)=x−3 f(x₀)=−6 => P= (2,−6) => −6=2a+b a=f'(x₀) = −1 => −6=−2+b => b=−4 ⇒ styczna: y=2a−4 czy robię to dobrze? co dalej? nie mam już pomysłu, utknąłem na dobre.

ICSP: źle wyznaczona styczna.

orzech: do którego momentu jest dobrze? y=2a+b, czyli f'(x₀)=2, dobrze myślę? nie mam pomysłu, proszę o wskazówkę.

orzech: i teraz: 2=x₀−3 ⇒ x₀=−1; f(x₀)=1,5

orzech: y=2x+b

3		5
	=2*2+b ⇒b=−
2		2

y=2x−{5}{2} teraz dobrze?

orzech:

	5
poprawiam: y=2x−
	2

ICSP: Wzór na styczną do wykresu funkcji f w punkcie x₀ y = f'(x₀)(x − x₀) + f(x₀)

orzech: w takim razie: a: f'(f₀)=−1 b: f(x₀)−f'(x₀)*x₀=−6−(−1)*2=−6+2=4 y=−x+4 teraz się zgadza?

orzech: oczywiście nie +4 tylko −4; y=−x−4

ICSP: f'(x) = x − 3 f'(2) = 2 − 3 = −1

	1
f(2) =		* 22 − 6 −2 = 2 − 6 − 2 = − 6
	2

y = −(x − 2) − 6 = −x + 2 − 6 = −x − 4

ICSP: działaj dalej

orzech: nie wiem czy dobrze myślę − styczną mam przyrównać do f(x), wyznaczyć x, następnie podstawić do jednego z tych równań i wyznaczyć y − będzie to punkt przecięcia? co dalej?

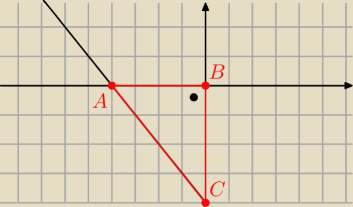
ICSP: Czego potrzebujesz aby wyliczyć pole trójkąta ABC ?

orzech: wyznaczyłem tenże punkt przecięcia czyli (−2,−2), choć nie wiem, czy był potrzebny; wyznaczam punkty: A(−4,0), B(0,0), C(0,−4);

	1		1
i teraz: Ptr.=		|(xB−xA)(yC−yA)−(yB−yA)(xC−xA)|=		=|4*(−4)−0|=8
	2		2

czyli udowodnione, zgadza się? dzięki za nadzorowanie, ICSP