jednokładność orzech: jednokładność: 1. odcinek A₁B₁ jest obrazem odcinka AB w jednokładności o środku O(0,0) i skali k. Wyznacz współrzędne środka E odcinka A₁B₁, jeśli: a) A(−20,6), B(10,4); k=3 2. odcinek A₁B₁ jest obrazem odcinka AB w jednokładności J o rodku w punkcie S(−2, −1) i skali k. Wyznacz współrzędne końców odcinka A₁B₁, jeśli: a) A(10,−6), B(−1, 4) k= −5 z góry dziękuję za pomoc, męczę tę jednokładność a i tak mi nic nie wychodzi; jeśli ktoś zna jakiś dobry "poradnik", gdzie mogę cokolwiek się dowiedzieć o tejże, to proszę o podanie linka, ja nie mogę nic konkretnego znaleźć, a na lekcji się nie skupialiśmy zbytnio na jednokładności(tylko pół lekcji na ten temat...), a rozszerzona matura, jak to rozszerzona − może się wszystko na niej pojawić.

Eve: 1. znajdź środek AB

orzech: śrAB: (−5,5), teraz muszę przemnożyć to przez k=3?

Mila: a) S=(0,0) A(−20,6), B(10,4) k=3 środek AB:

	−20+10		6+4
P=(xs,ys)=		,		)=(−5,5)
	2		2

J³_O(P)=P' P'(x,y)=(3*(−5),3*5)=(−15,15)

Eve: w jednokładności zalezność masz taką P(x,y)→→k→→P'(kx,ky), ale tylko o środku (0,0)

orzech: ok dzięki, z drugim też już dałem sobie radę, ale nadal nic nie łapię, robię to tylko podstawiając pod wzory

Eve: bo na tym to polega, jednokładność to powiększanie lub pomniejszanie w zależności od skali nie było w gimnazjum?

Mila: b) Tu bardziej problem skomplikowany. Korzystamy z definicji jednokladności. S(−2, −1) −środek jednokładności: k=−5 skala jednokładności. A(10,−6), B(−1, 4) SA₁^→=k*SA^→⇔ SA^→=[10+2,−6+1]=[12,−5] SA₁^→=[x+2,y+1] [x+2,y+1]=−5*[12,−5] x+2=−60 y+1=25 x=−62 y=24 A₁=(−62,24 W podobny sposób oblicz wsp. B₁

orzech: może i było, ale nawet jeśli, to niewiele pamiętam x) myślę, że powinniśmy więcej czasu poświęcić na to też w liceum, a nie zrobić 2 zadanka z podręcznika i po 20 minutach przejść na inny temat. pozostaje mieć nadzieję, że nie będzie tego na maturze.. mimo wszystko jeszcze spróbuję coś o tym poczytać. pzdr.

orzech: dzięki Mila za rozpisanie po kolei co i jak, widzę już trochę więcej co skąd i dlaczego

Mila: Punkty są takie, że trudno tu na forum zilustrować, w przypadku mniejszych wsp. narysuję w układzie, to zrozumiesz.

orzech: chwilę mi się zeszło, musiałem zrobić inhalację Mila, w takim razie: b) A(0,6), B(−4,0), k=3; S(−2,−1) → SA=[2,7] → SA₁=[x+2,y+1] x+2=6 ⇒ x=4 y+1=21 ⇒y=20 → A₁(4,20) → SB=[−2,1] → SB₁=[x+2,y+1] x+2=−6 ⇒ x=−8 y+1=3 ⇒ y=2 B₁(−8,2) proszę w takim razie o to rozrysowanie w układzie, bo na razie umiem jedynie podstawić do schematu x)

Eve: zapomniałes o skali SA₁=k*SA [x+2,y+1]=3*[2,7]

orzech: Eve, uwzględniłem skalę, jednak w pamięci już obliczyłem 3*2 i 3*7

Eve: fakt, nie zauwazyłam to juz rozumiesz?

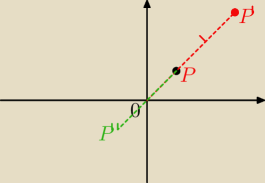
Eve: k=3 P(1,1) P'(3,3) k=−1 P"=(−1,−1)

orzech: częściowo; podstawy jednokładności chyba już zaczynam rozumieć, zagłębię się zatem zaraz w zadania bardziej zaawansowane x) a jeszcze pytanie − czy chcąc przedstawić to na układzie współrzędnych, powinienem użyć do tego cyrkla? w jaki sposób to zrobić?

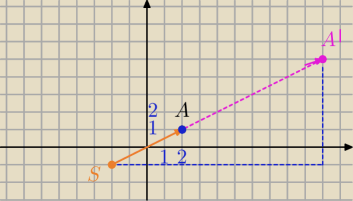
Mila: Przykro mi ale w tej skali nie dam rady. niech A=(2,1) S=(−2,−1), k=3 SA^→=[4,2] SA'^→[x+2,y+1]=3*[4,2]=[12, 6] x+2=12 y+1=6 x=10 y=5 A'=(10,5)

Eve: zdecydowanie tak, odległosci odkładasz ZAWSZE OD ŚRODKA JEDNOKŁADNOŚCI wejdź na stronę matmagwiazdy.pl i poszukaj tam jednokładności, gościu jest rewelecyjny

orzech: ok, dziękuję Eve i Mila, poczytam, pooglądam i porozwiązuję jeszcze zadania, i mam nadzieję, że jednak to opanuję − w razie dalszych problemów, zgłoszę się ponownie x) dzięki jeszcze raz.

Eve: na tej stronie łopatologicznie ci powie jak to jest z nią

Agantkaaa: Oblicz wartość wyrażenia jeśli wiadomo że a+b=1 i ab=−6 (a−1)(b−1) ; (a+4) (b+4) ; (a−5) (b−5)