odcinki wyznaczone przez punkt stycznosci lama: W trapez ABCD wpisano okrąg o promieniu równym 12. Ramię BC tegoż trapezu ma długość 25. Jakie długości mają odcinki wyznaczone na ramieniu BC przez punkt styczności S ?

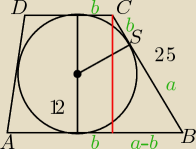
Godzio: 25=a+b 25²−24² = (a−b)² 49=(a−b)² a−b=7 25=a+b 7=a−b −> a=7+b 25=7+2b 18=2b b=9 7=a−9 a=16

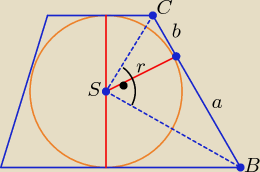
Bogdan: Albo korzystamy z faktu, że trójkąt BCS jest prostokątny i wówczas: r² = ab. Rozwiązujemy układ równań przy założeniach: a > 0 i b > 0: a + b = 25 i 144 = ab

Godzio: zawsze tak jesr że odcinki łączące końce dłuższego ramienia trapezu z środkiem okręgu wpisanego w ten trapez tworzą kąt prosty ?

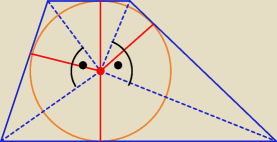
Bogdan: Każdego ramienia, nie tylko dłuższego, o ile okrąg jest wpisany w trapez.