POMOCY
Wojtek: wewnątrz trójkąta ABC wybrano dowolny punkt S. Uzasadnij, że /<CSB/ > /<CAB/.
22 lis 23:02
Basia:
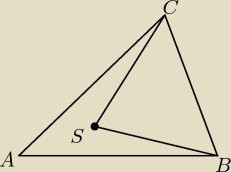
|∡CBS| < |∡CBA|
−|∡CBS| > −|∡CBA|
|∡BCS| < |∡BCA|
−|∡BCS| > −|∡BCA|
|∡CSB| = 180−|∡CBS|−|∡BCS| > 180−|∡CBA|−|∡BCA| = |∡CAB|
22 lis 23:16
AROB:
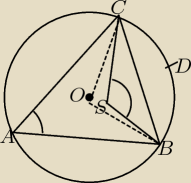
Po opisaniu okręgu na trójkącie ABC, kąt CAB jest kątem wpisanym opartym na łuku BDC.
Kąt środkowy BOC oparty na tym samym łuku jest 2 razy większy od kąta CAB . Także każdy inny
kąt oparty na tym samym łuku, mający wierzchołek w dowolnym punkcie wewnętrznym ΔABC (także w
punkcie S) jest większy od kąta CAB.
22 lis 23:25
 |∡CBS| < |∡CBA|
−|∡CBS| > −|∡CBA|
|∡BCS| < |∡BCA|
−|∡BCS| > −|∡BCA|
|∡CSB| = 180−|∡CBS|−|∡BCS| > 180−|∡CBA|−|∡BCA| = |∡CAB|
|∡CBS| < |∡CBA|
−|∡CBS| > −|∡CBA|
|∡BCS| < |∡BCA|
−|∡BCS| > −|∡BCA|
|∡CSB| = 180−|∡CBS|−|∡BCS| > 180−|∡CBA|−|∡BCA| = |∡CAB|
 Po opisaniu okręgu na trójkącie ABC, kąt CAB jest kątem wpisanym opartym na łuku BDC.
Kąt środkowy BOC oparty na tym samym łuku jest 2 razy większy od kąta CAB . Także każdy inny
kąt oparty na tym samym łuku, mający wierzchołek w dowolnym punkcie wewnętrznym ΔABC (także w
punkcie S) jest większy od kąta CAB.
Po opisaniu okręgu na trójkącie ABC, kąt CAB jest kątem wpisanym opartym na łuku BDC.
Kąt środkowy BOC oparty na tym samym łuku jest 2 razy większy od kąta CAB . Także każdy inny
kąt oparty na tym samym łuku, mający wierzchołek w dowolnym punkcie wewnętrznym ΔABC (także w
punkcie S) jest większy od kąta CAB.