monotoniczność.
Combo: Zbadać monotonicznośc funkcji
po obliczeniu wyszło mi że
funkcja rosnąca dla (1;+
∞)
Funkcja malejaca dla (−
∞;0)U(0,1)
Minimum w punkcie x=1
y=e
Dobrze to jest?
26 sty 18:37
Janek191:
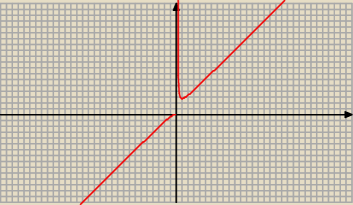
26 sty 18:55
Combo: Dziwne ...
Bo jak zrobiłem to w tabelce to wyszło mi minimum

Właśnie dla x=1 y=e....
26 sty 19:03
Janek191:
Jest minimum lokalne dla x = 1 równe ymin = e
26 sty 19:06
Combo: No właśnie,tak mi wyszło ,więc wszystko dobrze?

26 sty 19:07
Janek191:
Dla x < 0 jest y < 0
26 sty 19:07
Janek191:
Z wykresu wynika, ze funkcja jest rosnąca w ( − ∞ ; 0 )
26 sty 19:08
Combo: | | 1 | | 1−x | |
f(x)=e do potęgi |
| [ |
| ] |
| | x | | x | |
funkcja rosnąca dla f
,x>0
1−x>0
x<1

?
26 sty 19:15
Combo: Może ktoś sie wypowiedzieć?
26 sty 21:34
john2: Ale, o co chodzi? Co tam jest w pierwszej linijce?
26 sty 21:38
Combo: | | 1 | |
PRzecież jest napisane y=xe do potęgi |
| |
| | x | |
26 sty 21:42
john2: x(x − 1) > 0
y' > 0 dla x(−
∞,0)u(1, +
∞)
26 sty 21:50
Combo: Czy to jest dobrze?
26 sty 22:07
john2: Czy co jest dobrze?
26 sty 22:08
Combo: To co zrobiłeś

26 sty 22:13
Combo: Bo pierwszy wers sie nie zgadza...
| | x−1 | |
Ja nie uwzględniłem x tylko po prostu |
| >0 .....  i tak samo dla f ,(x)<0 |
| | x | |
26 sty 22:14
john2:
mnożę obustronnie przez x
2, przez x nie mogę, bo x może być ujemny, i nie wiem czy się nie
zmieni znak nierówności
x(x − 1) > 0
26 sty 22:19
john2: | | 1 | |
ex(1 − |
| ) to oczywiście pochodna funkcji xe1/x |
| | x | |
26 sty 22:23
Combo: No wiem ,ale źle to zrobiłem i już wszystko klapa.... :⊂
26 sty 22:23
john2: albo i nie, moment
26 sty 22:23
Combo: To nie jest pochodna tej funkcji.
Powinno być e1/x [...]
26 sty 22:24
john2: | | 1 | |
pochodna to e1/x(1 − |
| ), ale to i tak nic nie zmienia |
| | x | |
26 sty 22:25
Combo: Wiem ,ale dla ścisłości

Kurde,szkoda, bo taki błąd i wszystko źle...
26 sty 22:27
26 sty 22:31
Combo: Nie zrobiłem niestety,nie lubie takich funkcji .....

26 sty 22:39

 Właśnie dla x=1 y=e....
Właśnie dla x=1 y=e....

 ?
?

 i tak samo dla f,(x)<0
i tak samo dla f,(x)<0  Kurde,szkoda, bo taki błąd i wszystko źle...
Kurde,szkoda, bo taki błąd i wszystko źle...
