Stereo Frost: Podstawą ostrosłupa jest trójkąt ABC w którym bok AB ma długość a,a kąty wewnętrzne do niego przyległe mają miarę β γ. Krawędź boczna wychodząca z wierzchołka C ma miarę d i jest prostopadła do podstawy. Oblicz objętość brył na które ten ostrosłup dzieli płaszczyzna

	d
równoległa do podstawy i oddalona od niej o		. Jakieś pomysły?
	3

Frost: ?

Mila: Z czym masz problem?

Frost: nie mogę określić jakoś tych kątów ładnie na rysunku. Dopiero zaczynam ten dział

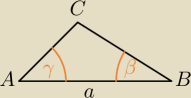
Mila: Może kąt był α? 1) oblicz pole ΔABC. 2) oblicz V₀ 3) Zauważ podobieństwo ostrosłupa "odciętego" płaszczyzna równoległą do ΔABC. 4) skorzystaj z własności brył podobnych.

Frost: czyli te kąty nie są w przestrzeni tylko w płaszczyźnie?

Mila: W podstawie.

Frost: Okey dzięki, jutro zrobię dzisiaj już nie mam sił

Mila: Będę śledzić.

Frost: Odpowiedzi: Objętość odciętego stożka

8a2*sinβ*sinγ*d
162*sin(β+γ)

Objętość dolnej figury

19a2*sinβ*sinγ*d
162*sin(β+γ)