zastosowanie pochodnych sebol:

	2x
określ monotonicznośc funkcji i ekstrema lokalne funkcji f(x)=		. Znam kolejność
	1−lnx

"kroków" jakie trzeba zrobić aby rozwiazac takie zadanie, ale po policzeniu pochodnej nie potrafie narysować tego wykresu przez co nie umiem okreslić czy nastąpiła zmiana znaku w pkt stacjonarnych... przeszkadza ten ln(X). Pomoże ktoś zrobić ten przykład?

Dawid:

	2x		2lnx−2
f'(x)=		=
	1−lnx		(1−lnx)2

2lnx−2=0 2lnx=2 lnx=1 lnx=lne x=e

J: źle pochodna ...

Dawid: W mianowniku ma być −2lnx+2

Dawid: ?

Dawid: A dobra już wiem −2lnx+4

J:

	2(1−lnx) + 2
f'(x) =
	(1−lnx)2

Dawid: Zatem: −2lnx+4=0 −2lnx=−4 lnx=2 lnx=lne² x=e²

J: znak pochodnej zależy od znaku y = 2(2 − lnx) .... i widać,że w x = e² zmienia znak ...

sebol: a jeśli chodzi o monotoniczność?

sebol: Jak określić taką monotoniczność gdy nie widzie kiedy wykres jest pod a kiedy nad osią x? a w tym obliczonym przypadku jak dojść czy jest to max czy min lokalne?

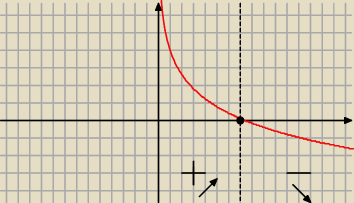
Dawid: Narysuj sobie wykres przybliżony wykresu −2lnx+4=0