romb i obwód powstałego w nim rombu. goryl: Kąt rozwarty rombu ABCD ma miarę 120°, a bok rombu jest krótszy od dłuższej przekątnej o 2 cm. Wiedząc, że punkt O jest punktem przecięcia się przekątnych rombu, oblicz obwód czworokąta, którego wierzchołkami są środki odcinków AO, BO, CO, DO. Serdecznie proszę o pomoc.

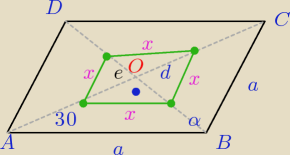
Godzio: e−> krótsza przekątna d−> dłuższa przekątna a−> bok rombu α=120^o d=a+2 trójkąt AOB: boki:

d		e
	, a,
2		2

	e   2
sin30=
	a

a=e

d2		a2
	+		=a2
4		4

d²=3a² (a+2)²=3a² a²+4a+4=3a² −2a²+4a+4=0 Δ=16+32=48 √48=4√3

	−4−4√3
a1=		=1+√3
	−4

	−4+4√3
a2=		=1−√3 <−odżucamy
	−4

a=1+√3 wiemy że odcinek łączący środki 2 boków trójkąta jest równoległy do 3 boku a jego wartość to połowa poku 3 czyli:

	1		1		1
x=		a=		+		√3
	2		2		2

l=4x=2+2√3

Godzio: tego e to nawet nie trzeba obliczać

goryl: dziękuję (;