dd
Hugo:
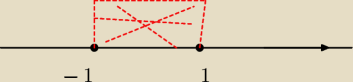
przebieg funkcji (okrojony) prosze mnie sprawdzić

1. Dziedzina
2. Asymptoty
3. Extremy
4. Wypuklosci
5. Tabelka
6. Wykres
y = x + sinx
1. Df: x e <−1; 1>
2. lim x−> −1
+ sinx + x =

nie da się
2. lim x−> +1
− sinx + x = ...

znowu nie ma asymptoty pionowej?
| | f(x) | | sinx | |
a = lim x−> +− oo |
| = lim x−> −+oo 1 + |
| = sin(oo) nie istnieje   mamy tu |
| | x | | x | |
nei skonczonosc przez nieskonczonosc dejupital nam nic nie da bedze cosinus nie skonczonosci
WIEC NIE MA ASYMPTOT ANI PIONOWYCH ANI POZIOMYCH

26 sty 12:48
J:
a dlaczego dziedzina to tylko <−1,1> ...?
26 sty 12:52
Hugo: a jaka

? pomocy
26 sty 12:55
Hugo: sinx jest ograniczony <−1 ; 1> a x nic nie zmienia
26 sty 12:56
kyrtap: R
26 sty 12:56
kyrtap: dziedziną sinx jest R a zbiorem wartości <−1,1>
26 sty 12:57
J:
przecież dziedziną funkcji sinx jes R
26 sty 12:57
Hugo: 
racja
26 sty 13:00
Hugo: ale tgx arctg ctg czy cos to juz nie !
26 sty 13:01
J:
y = cosx ... D = R
26 sty 13:01
Hugo: 
dz
26 sty 13:11
Hugo: czyli nie ma asymptot pionowych
26 sty 13:11
Hugo: a co z poziomymi

ukośnymi

a = lim x−> +− oo U{f(x)}{x)

26 sty 13:11
26 sty 13:12
Hugo: jak podstawie pod sinusa nie skonczonosc?
26 sty 13:12
26 sty 13:13
Hugo: nie istnieje?
26 sty 13:14
Hugo: :((
26 sty 13:20
26 sty 13:26
26 sty 13:33
26 sty 13:37
Hugo: [C[dwie grupy mam i w sumie 4 zadania]
y = sinx + x
y = ln(1+x2)
y = cosx −1
y = (x−1)ex
blagam o pomoc !
26 sty 14:09
john2: Gdzie jest problem?
26 sty 14:14
Hugo: Potrzebuje rozwiązać te 4 zadania, problem z pierwszym jak licze asymptoty ukośne z sinusem jak
to trzeba zrobic

?
26 sty 14:23
26 sty 14:28
john2: chyba tak:
| | x+sinx | | sinx | | 1 | |
limx−>±∞ |
| = limx−>±∞ [1 + |
| ] = limx−>±∞ [1 + sinx * |
| ] = |
| | x | | x | | x | |
[1 + funkcja ograniczona * 0 ] = [1 + 0] = 1
b nie ma
26 sty 14:30
Hugo: | | sin +−oo | |
bo jak licze a = lim f(x) / x to mam 1 + |
| i zeby sie równo wazyło z |
| | +−oo | |
| | sin +−oo | |
znalezionym w necie rozwiazaniem musi to dawac 1 wiec |
| sie zeruje  |
| | +−oo | |
26 sty 14:31
Hugo: aaaale sprytne razy zero

no dzięki
prosze zostań jeszcze na te 4 przyklady
26 sty 14:32
Hugo: okej wiec wyraz b
26 sty 14:34
john2: ok, ale mogę nie odpowiadać zbyt szybko
26 sty 14:34
Hugo: b = lim ... f(x) − ax
b= lim... sinx + x − x = sinx
sin(+−oo)

26 sty 14:34
26 sty 14:35
Hugo: tam widać że OY przebija w pkt 1 i −1 wiec b musi dać II rozwiązania
26 sty 14:36
Hugo: zatem lim x−> +−oo sinx = 1 v − 1? Tylko jak i wgl
26 sty 14:36
Hugo: pochodne:
pochodne
y' = 1 + cosx
1+ cox = 0
cosx = −1
x = pi + 2kpi
czy to bedzie miec extrema ? bo rosnie spada rosnie spada '
y'' = −sinx
−sinx = 0
sinx = 0
x = kpi
Dobrze

tabelke sb odpuszcze ale bo mam ~2,5h

wykres mam, ale zapytam sie czy są jakies extremum
albo uskoki wklęsłości

funkcja jest okresowa
26 sty 14:41
john2: Nie wiem.
b = limx−>±∞ (x + sinx − x) = limx−>±∞ sinx a to chyba nie ma granicy. Na tym rysunku nie
powiedziałbym, że to są asymptoty ukośne. Wykres funkcji ma się zbliżać do asymptoty np w plus
nieskończoności. Tutaj się nie zbliża.
26 sty 14:43
john2: Zobacz kiedy y' > 0 i będziesz wiedzieć, że kandydat pi plus pi/2 może być ekstremum.
to samo z y''
y'' > 0, gdy sinx < 0
dla tych x funkcja wesoła
y'' < 0, gdy sinx > 0
dla tych x funkcja funkcja wesoła
jest zmiana znaku y'' wokoł kpi
26 sty 14:48
john2: Poprawka:, że nie może być ekstremum
26 sty 14:48
Hugo: y = ln(1+x2)
y = cosx −1
y = (x−1)ex
y = ln(1+x2)
1+x
2 > 0
x
2> −1
x e R
nie ma pionowych
| | f(x) | | ln (1+x2) | |
a = |
| = |
| = [oo]/[oo] Hospital ale tylko dla x−> + oo bo dla ujemnego |
| | x | | x | |
ni ma

26 sty 14:48
john2: Poprawka2 że π + 2kπ nie może być ekstremum
26 sty 14:49
john2: Poprawka3: dla y'' < 0
funkcja smutna
26 sty 14:50
john2: lim przy x − > minus nieskończoności też ma sens, bo x jest do kwadratu
26 sty 14:52
Hugo: f''(x) = (1 + cos x)' = − sin x
(f''(x) = 0) ⇔ (− sin x = 0) ⇔ (x ∈ {kπ, k ∈ Z})
(f''(x) > 0) ⇔ (− sin x > 0) ⇔ (sin x < 0) ⇔ (x ∈ ((2k − 1)π, 2kπ), k ∈ Z})
(f''(x) < 0) ⇔ (− sin x < 0) ⇔ (sin x > 0) ⇔ (x ∈ (2kπ,(2k + 1)π), k ∈ Z})
26 sty 14:52
Hugo: a moglbys mi napisac tabelke

?
26 sty 14:53
john2: Nie wiem, jak się robi te przedziały w tabelkach przy funkcjach trygonometrycznych, pomyślę.
26 sty 15:02
john2: Zrobiłbym to bez tabelki.
y'>0 dla x ∊R \ {π+2kπ}
f(x) ↗ x ∊R
y'' > 0 dla x ∊ (0 + 2kπ, π + 2kπ)
dla tych x f(x) ∪
y'' < 0 dla x ∊ (π + 2kπ, 2π + 2kπ)
dla tych x f(x) ∩
Punkt przegięcia (kπ, kπ)
26 sty 15:19
john2: Kurde, sorry, źle te przedziały wyznaczyłem.
26 sty 15:21
Hugo: juz ok ok

mam wszystko z tym
26 sty 15:22
Hugo: f jest wypukła dla x ∈ ((2k − 1)π, 2kπ), k ∈ Z}, wklęsła dla x ∈
(2kπ,(2k+1)π), k ∈ Z}, punkty przegięcia są elementami zbioru {kπ, k ∈
Z}.
26 sty 15:22
Hugo: jest rosnąca nie ma extremów, są pkt przegięć

1,5h zostalo mi

zad 2

?
26 sty 15:23
john2: Będzie dokładnie na odwrót, y'' > 0 dla tego drugiego przedziału, y'' < 0 dla tego pierwszego
26 sty 15:24
john2: No to jedź. Tak jak pisałem ukośna w minus nieskończoności też może być.
26 sty 15:27
Hugo: ln(x2 + 1)
26 sty 15:28
Hugo: post 14:48
26 sty 15:29
Hugo: b dla x −> +oo
lim x−>oo ln (x
2 +1) = nie istnieje

⇔ brak ukośnych?
[ln (oo) = oo]

26 sty 15:30
john2: No już się odniosłem do tego, minus nieskończoność też uwzględnij
26 sty 15:31
john2: tak, brak ukośnych
26 sty 15:31
Hugo: | | 2x | |
y' = |
| −−−−−> x = 0 |
| | x2+1 | |
| | −2x2 +2 | |
y'' = |
| −−−−−−−−> x = 1 v x = −1 |
| | x2 +1 | |
26 sty 15:32
Hugo: no tak tak dla x −> −oo nie ma ! juz przy obliczaniu 'a' bo ln(−oo) nie ma

26 sty 15:33
Hugo: a wykres bys umial tak mniejwięcej? jak nie to lecimy dalej

26 sty 15:33
26 sty 15:34
Hugo: TO lecimy do 3
 y = cosx −1
y = cosx −1
y = (x−1)e
x
26 sty 15:36
Hugo: dziedzina
x e R
asymptoty
brak pionowych
as. ukośne
| | cos(+−oo) −1 | |
lim x−>+− f(x) / x = NIE MA  ponownie  |
| |
| | +−oo | |
26 sty 15:37
john2: Jeszcze raz powtarzam. Minus nieskończoność ma sens, bo ln(1 + (−∞)2) = ln(1 + ∞) = ln(∞)
26 sty 15:39
john2: Masz wszystkie dane do wykresu. Zaznacz ekstrema, punkty przegięcia, patrz gdzie funkcja
∪/∩ i ↗/↘
26 sty 15:41
john2: f(x) = cosx − 1 nie będzie mieć asymptot ukośnych, bo jest to funkcja okresowa.
26 sty 15:43
Hugo:
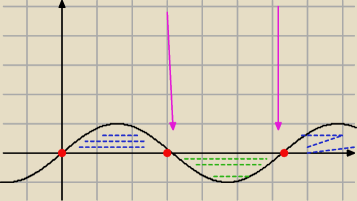
y' = −sinx
−sinx = 0
sinx = 0 , x = kpi , k e C
extremy są

chyba są

w pkt x = kpi
26 sty 15:45
Hugo: racja nie zauważyłem oo2 dzieki : ))
odpuszcze sb tabelke ;x chce jeszcze te przykladdy zrobic malo czasu mam tabelka prosta
26 sty 15:46
Hugo: y'' = −cosx
sytuacja podobna
−cosx = 0
cosx = 0
//tak mozna

robic? budować dla cosx = 0 wykres a nie dla −cosx

pkt przegięcia dla x = kpi
26 sty 15:49
john2: Narysowałeś sinx zamiast −sinx.
Są ekstrema co π, ale zauważ, że są to na przemian minima i maksima.
26 sty 15:50
Hugo: wiem wiem, −sinx a sinx w tym wypadku dla zera to to samo

26 sty 15:54
john2: Ale nie to samo, gdy badasz znak...
26 sty 15:55
john2: Pamiętaj, że badasz znak pochodnej, czyli rozwiązujesz nierówności:
− cosx > 0 oraz − cosx < 0
Możesz patrzeć na wykres cosx, ale wtedy patrzysz, gdzie indziej na wykres.
26 sty 15:59
john2: Poza tym, mam nadzieję, że nie zapominasz liczyć wartości funkcji dla ekstremów i punktów
przegięcia.
26 sty 16:00
john2: | | π | |
Punkt przegięcia to ( |
| + kπ, −1) |
| | 2 | |
26 sty 16:03
Hugo: tam sie zero równa
26 sty 16:04
Hugo: jak to pi/2 + kpi , −1
od pi/2 + kpi do −1? −1 jest bez kpi wiec wkońcu pi/2 + kpi przerosnie −1
26 sty 16:05
john2: to co napisałem to współrzędne punktu przegięcia, nie przedział
26 sty 16:06
Hugo: ach : )
26 sty 16:17
Hugo: no to tak sie zgadza

26 sty 16:17
Hugo: powiedz mi
y = (x−1)e
x
pionowych nie ma
ukośne:
| | (x−1)ex | |
dla x−>oo a= lim |
| = [oo]\[oo] |
| | x | |
Hospital
| | ex | |
lim x−>oo ex * x = |
| = 0  |
| | 1/x | |
| | ex | | oo | |
[ |
| ] −−−> [ |
| ] −> 0  |
| | 1/oo | | 0 | |
26 sty 16:21
john2: | | (x − 1)ex | | (x − 1) | |
lim x − >±∞ |
| = lim x − >±∞ |
| * ex |
| | x | | x | |
| | (x − 1) | |
lim x − >+∞ |
| * ex = [1 * ∞] |
| | x | |
| | (x − 1) | |
lim x − >−∞ |
| * ex = [1 * 0] |
| | x | |
26 sty 16:25
Hugo: 
aaaaaaaaaaaaaaaaa
26 sty 16:28
Hugo: wyraz b

26 sty 16:31
Hugo: ale tylko dla x−> −oo
(x − 1)ex − ax = ....
26 sty 16:32
Hugo: i wychodzi ze
| | 1 | | oo | |
−oo * |
| czyli Hospital |
| ale no to jedno trzeba do mianownika a nie wiem jak |
| | oo | | oo | |
26 sty 16:33
Hugo: 

26 sty 16:33
john2: | | x −1 | |
limx−>−∞ (x−1)ex = |
| teraz regułą |
| | | |
26 sty 16:35
Hugo: ja wrzucalem x−1 do mianownika, mozna tez?
26 sty 16:36
Hugo: 1/ e
−oo = e
oo prawda

26 sty 16:36
john2: można, ale chyba wtedy Ci nic to nie da,
26 sty 16:38
Hugo: Hostpital
| 1 | | 1 | | 1 | |
| = |
| = |
| = ex = |
| 1/e2x * ex | | ex/e2x | | e−x | |
a ze mamy x−> oo
e
x = 0 dobrze?
ukosna
y = 0
26 sty 16:40
Hugo: ale jak robiles pochodną mianownika
| 1 | | 1 | |
| = − |
| * ex czyz nie? |
| ex | | e2x | |
26 sty 16:43
26 sty 16:43
john2: tak
26 sty 16:44
Hugo: wiec masz źle ;> a ja zgubilem minus

26 sty 16:47
Hugo:
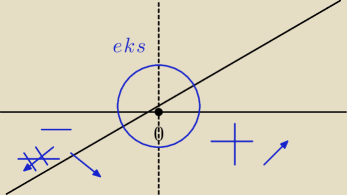
w miedzy czasie pochodną
y = (x−1)e
x
y' = e
x + (x−1)e
x
y' = 0 /dzieli przez e
x
1 + x − 1 = 0
x = 0
ekstrema minimalna w pkt (0, −e
x)
26 sty 16:51
john2: To co napisałem o 16:38 było odpowiedzią na Twoje pytanie z 16:36, nie liczyłem tam pochodnej.
26 sty 16:53
john2: Skąd ta druga współrzędna ekstremum?
26 sty 16:54
Hugo:

y'' = e
x + e
x + (x−1)e
x
y'' = 0 /dzielimy przez e
x
x = −1
pp ( −1, −2e
x)
26 sty 16:55
Hugo: obliczylem z f(x) : > to sie podstawia

(0...
f(0) = (0 − 1) e
x
26 sty 16:56
Hugo: ach ok

26 sty 16:57
john2: Druga współrzędna ekstremum to −1
| | −2 | |
Druga współrzędna punktu przegięcia to |
| |
| | e | |
26 sty 17:00
Hugo: jak to druga jest jedno rozwiazanie
26 sty 17:08
Hugo: a racja bo ja wydzielillem przez ex a nie wolno potem dalem do jednego nawiasu i jest ex(x+1)
lece do goscia trzymaj kciuki dzieki wielkie !
26 sty 17:10
john2: możesz dzielić przez ex
drugą współrzędną ekstremum/punktu przegięcia wyznaczasz, podstawiając do wzoru funkcji
odpowiednio x = 0 (minimum) i x = −1 (punkt przegięcia)
26 sty 17:14
john2: tzn nie wolno dzielić we wzorze funkcji, ale w równaniu y = 0 lub nierówności y > 0, y < 0
możesz dzielić przez ex, bo ex > 0 zawsze.
26 sty 17:16
Hugo: na kolokwium byly takie funkcjie
ln(x
2+1)
2x + arctg

mysle ze dst bedzie oddalem mu 4 x a5
26 sty 19:37
john2: 
dobrze, że żadnych sinusów, bo z nimi można się pogubić
26 sty 19:57
 przebieg funkcji (okrojony) prosze mnie sprawdzić
przebieg funkcji (okrojony) prosze mnie sprawdzić  1. Dziedzina
2. Asymptoty
3. Extremy
4. Wypuklosci
5. Tabelka
6. Wykres
y = x + sinx
1. Df: x e <−1; 1>
2. lim x−> −1+ sinx + x =
1. Dziedzina
2. Asymptoty
3. Extremy
4. Wypuklosci
5. Tabelka
6. Wykres
y = x + sinx
1. Df: x e <−1; 1>
2. lim x−> −1+ sinx + x =  nie da się
2. lim x−> +1− sinx + x = ...
nie da się
2. lim x−> +1− sinx + x = ...  znowu nie ma asymptoty pionowej?
znowu nie ma asymptoty pionowej?

 mamy tu
mamy tu
 ? pomocy
? pomocy
 racja
racja
 dz
dz
 ukośnymi
ukośnymi a = lim x−> +− oo U{f(x)}{x)
a = lim x−> +− oo U{f(x)}{x) 


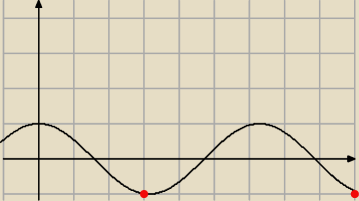 pochodne
y' = 1 + cosx
1+ cox = 0
cosx = −1
x = pi + 2kpi
czy to bedzie miec extrema
pochodne
y' = 1 + cosx
1+ cox = 0
cosx = −1
x = pi + 2kpi
czy to bedzie miec extrema  ? bo rosnie spada rosnie spada
? bo rosnie spada rosnie spada 



 '
y'' = −sinx
−sinx = 0
sinx = 0
x = kpi
'
y'' = −sinx
−sinx = 0
sinx = 0
x = kpi
 http://scr.hu/2pdc/szeyp
http://scr.hu/2pdc/szeyp
 ?
?

 no dzięki
prosze zostań jeszcze na te 4 przyklady
no dzięki
prosze zostań jeszcze na te 4 przyklady

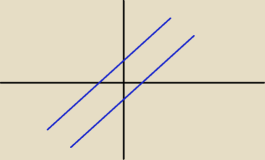 zobacz na ten link
http://scr.hu/2pdc/rifnk
zobacz na ten link
http://scr.hu/2pdc/rifnk
 tabelke sb odpuszcze ale bo mam ~2,5h
tabelke sb odpuszcze ale bo mam ~2,5h  wykres mam, ale zapytam sie czy są jakies extremum
albo uskoki wklęsłości
wykres mam, ale zapytam sie czy są jakies extremum
albo uskoki wklęsłości funkcja jest okresowa
funkcja jest okresowa

 ?
?
 mam wszystko z tym
mam wszystko z tym
 1,5h zostalo mi
1,5h zostalo mi zad 2
zad 2  ?
?
 ⇔ brak ukośnych?
[ln (oo) = oo]
⇔ brak ukośnych?
[ln (oo) = oo] 


 y = cosx −1
y = (x−1)ex
y = cosx −1
y = (x−1)ex
 ponownie
ponownie
 y' = −sinx
−sinx = 0
sinx = 0 , x = kpi , k e C
extremy są
y' = −sinx
−sinx = 0
sinx = 0 , x = kpi , k e C
extremy są  chyba są
chyba są  w pkt x = kpi
w pkt x = kpi
 robic? budować dla cosx = 0 wykres a nie dla −cosx
robic? budować dla cosx = 0 wykres a nie dla −cosx pkt przegięcia dla x = kpi
pkt przegięcia dla x = kpi




 aaaaaaaaaaaaaaaaa
aaaaaaaaaaaaaaaaa





 w miedzy czasie pochodną
y = (x−1)ex
y' = ex + (x−1)ex
y' = 0 /dzieli przez ex
1 + x − 1 = 0
x = 0
ekstrema minimalna w pkt (0, −ex)
w miedzy czasie pochodną
y = (x−1)ex
y' = ex + (x−1)ex
y' = 0 /dzieli przez ex
1 + x − 1 = 0
x = 0
ekstrema minimalna w pkt (0, −ex)
 y'' = ex + ex + (x−1)ex
y'' = 0 /dzielimy przez ex
x = −1
pp ( −1, −2ex)
y'' = ex + ex + (x−1)ex
y'' = 0 /dzielimy przez ex
x = −1
pp ( −1, −2ex)
 (0...
f(0) = (0 − 1) ex
(0...
f(0) = (0 − 1) ex

 mysle ze dst bedzie oddalem mu 4 x a5
mysle ze dst bedzie oddalem mu 4 x a5
 dobrze, że żadnych sinusów, bo z nimi można się pogubić
dobrze, że żadnych sinusów, bo z nimi można się pogubić