nierówbność Matmat: |2x−2| / |x−4| > 4

Matmat: mam problem z tą nierównością wymierną z wartością bezwzględną. Pomoże ktoś ?

Draghan: 1. Dziedzina. 2. Nierówności wymierne zawsze powinno się rozwiązywać, sprowadzając do wspólnego mianownika (chyba że charakter zadania pozwala na wskazanie wyniku szybciej).

|2x−2|		|2x−2|		|2x−2|		4|x−4|
	> 4 ⇒		− 4 > 0 ⇒		−		> 0 ⇒
|x−4|		|x−4|		|x−4|		|x−4|

	|2x−2| − 4|x−4|
⇒		> 0 ⇔ ( |2x−2| − 4|x−4| )*( |x−4| ) > 0
	|x−4|

3. Rozpisujesz przedziały dla wartości bezwzględnych i rozwiązujesz przekształconą nierówność w przedziałach, opuszczając wartości bezwzględne.

Tadeusz: x≠4

	2x−2
|		|>4
	x−4

2x−2		2x−2
	<−4 lub		>4
x−4		x−4

2x−2+4x−16		2x−2−4x+16
	<0		>0
x−4		x−4

6(x−3)(x−4)<0 −2(x−7)(x−4)>0 x∊(3, 4) x∊....... i suma tych przedziałów x∊ ....

Matmat: Dzięki wielkie za pomoc, rozumiem a jak z przykladem 3/|x|−1 ≥2

Matmat: jak sobie z tym poradzić ?

Tadeusz: ... to może zapisz go porządnie

3		3
	−1≥2 czy		≥2
|x|		|x|−1

Matmat: 2 zapis

Matmat:

3
	≥ 2
|x|−1

Matmat: pomożecie ?

Tadeusz: x≠−1 x≠1

3
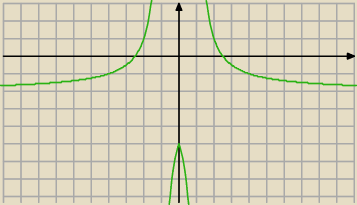
	−2≥0
|x|−1

3−2|x|+2
	≥0 ⇒ (2|x|−5)(|x|−1)≥0 ⇒ 2(|x|−2,5)(|x|−1)≥0
|x|−1

...dalej poradzisz?

J: 1) założenie: x ≠ 1 i x ≠ −1

	3
2) dla x ≥ 0 masz :		≥ 2
	x−1

	3
dla x < 0 masz:		≥ 2
	−x −1

Matmat: tak dzięki

Matmat: Dzięki wielkie za pomoc, jak zawsze nie zawodni . Na prawdę pomogliscie pozdrawiam