przekrój ostrosłupa
xyz: Przez krawedz AB podstawy ostroslupa prawidłowego trojkatnego ABCD poprowadzono
płaszczyznę, do której należy środek S krawędzi CD. Wiedząc, że otrzymany przekrój tworzy
z płaszczyzną podstawy kąt 45°, oblicz cosinus kąta ASB.
W odpowiedziach: 5\11
Bardzo proszę o pomoc.
25 sty 20:43
Eve: rozpracowałam rysunek, ale mam za dużo niewiadomych

25 sty 21:03
Eve:
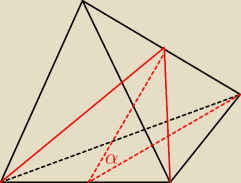
25 sty 21:04
Tadeusz:
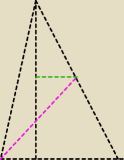
i teraz masz tylko jedną ... i da się policzyć kąt przekroju
25 sty 21:35
xyz: Nie rozumiem tego drugiego rysunku.
25 sty 21:42
Tadeusz:
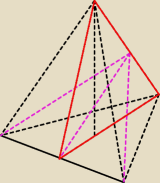
to ten przekrój
25 sty 21:54
Eve: aha, to sobie skomplikowaliśmy zadanko

25 sty 21:56
Tadeusz:
Nie Ewe ... Twój rysunek jest ok
Ja opisując swój pierwszy rysunek niezręcznie się wyraziłem.
Ten pierwszy szkic to szczegół zarysowany na czerwono Twojego rysunku.
25 sty 22:02
Eve: aha, myślałam, że źle wyznaczyłam przekrój
25 sty 22:04
groszek:
Rysunek Evę jest nieporady.
Tadeuszu, znasz się na rysunku, że autorytatywnie stwierdzają, że rysunek jest ok?
25 sty 22:27
Mila:
Rysunek Eve , bardzo dobry. Uwaga Tadeusza cenna.
Brak oznaczeń. Nie mogę dać dalszej wskazówki.
25 sty 23:17
Eve: ale oznaczenia są standardowe, od lego dolnego wierzchołka, niezgodnie z ruchem wskazówek
zegara

25 sty 23:23
Mila:
Zrobić nowy rysunek?
25 sty 23:24
Eve:
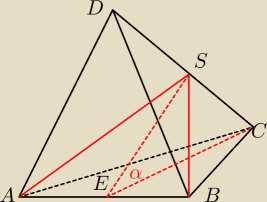
się nie męcz
25 sty 23:26
groszek:
Tu są poprawne rysunki: www.matemaks.pl/stereometria.php
25 sty 23:37
Tadeusz:
...groszek ... płacą ci chociaż grosze za tą kryptoreklamę?
25 sty 23:42
Mila:
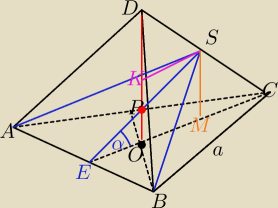
α=45
o
| | 1 | | 1 | a√3 | | a√3 | |
|EO|= |
| * |OC|= |
|
| = |
| |
| | 2 | | 3 | 2 | | 6 | |
| | 1 | |
SK||OC i |SK| = |
| * |OC| |
| | 2 | |
| | a√3 | |
ΔEOP≡ΔPKS− Δprostokątne równoramienne o przyprostokątnych równych |
| |
| | 6 | |
| | a√3 | | a√3 | |
|SM|=|EM|=|OK|=2* |
| = |
| |
| | 6 | | 3 | |
⇔
| | a√3*√2 | | a√6 | |
|ES|= |
| = |
| ponieważ ΔEMS−Δprostokątny równoramienny |
| | 3 | | 3 | |
Dalej z tw. cosinusów: ∡ASB=β
a
2=2|BS|
2−2|BS|
2*cosβ
Dokończy
xyz
25 sty 23:45
groszek:
Dla mnie to obca strona i przed chwilą znalazłem ją przez GOOGLE. Nie ma co się obrażać.
Rysunek to ważny element rozwiązania.
25 sty 23:53
xyz: Bardzooooo wam dziękuję (w szkole próbowaliśmy zrobić to zadanie przez dwie lekcje i nie
wyszło).
26 sty 11:05
Mila:
Co trzy głowy to nie jedna.

26 sty 15:51
Bogdan:
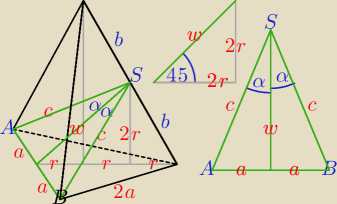
Podłączam się do trzech głów, co cztery głowy, to nie trzy

| | 1 | |
r − długość promienia okręgu wpisanego w trójkąt równoboczny, r = |
| *2a√3 ⇒ a = r√3 |
| | 6 | |
w = 2r
√2, c =
√a2 + w2 =
√3r2 + 8r2 = r
√11,
| | w | | 2r√2 | | 2√2 | |
cosα = |
| = |
| = |
| |
| | c | | r√11 | | √11 | |
| | 8 | | 5 | |
cos2α = 2cos2α − 1 = 2* |
| − 1 = |
| |
| | 11 | | 11 | |
26 sty 16:21
Mila:
Witam, Bogdanie, też tak rozwiązywałam, ale ze względu na cos (2α) "włączyłam" sposób jak
zapisałam.
Pozdrawiam.
Właśnie przyszedł do mnie uczeń.
26 sty 16:29
Bogdan:
Również pozdrawiam

26 sty 16:30
Kacper:

26 sty 16:30
Bogdan:
Jeśli podający zadanie nie określa, na jakim poziomie pracuje (podstawowym, czy
rozszerzonym), to nie rezygnuję z dogodnego i upraszczającego rozwiązanie narzędzia.
26 sty 16:34
Bogdan:
ale jeśli bez cos2α, to skorzystamy z pola trójkąta ABS (zostawiam miarę 2α i inne
oznaczenia z moich rysunków):
| | 1 | |
Pole P = |
| c2*sin2α oraz P = a*w |
| | 2 | |
| 1 | | 4√6 | |
| c2sin2α = a*w ⇒ 11r2*sin2α = 2*r√3*2r√2 ⇒ sin2α = |
| |
| 2 | | √11 | |
cos2α =
√ 1 − sin2α = ...
26 sty 16:44



 to ten przekrój
to ten przekrój


 się nie męcz
się nie męcz
 α=45o
α=45o

 Podłączam się do trzech głów, co cztery głowy, to nie trzy
Podłączam się do trzech głów, co cztery głowy, to nie trzy 

