Geometria analityczna
Dżepetto 18: | | 1 | |
W którym punkcie wykresu funkcji f(x)= |
| gdzie x ≠ 0 należy poprowadzić styczną do tego |
| | x2 | |
wykresu aby pole trójkąta ograniczonego tą styczną i osiami układu współrzędnych było równe

25 sty 17:28
Dżepetto 18: 
25 sty 19:14
Dżepetto 18: Nieśmiało liczę, że Pani Eta dojrzy ten post i po x kolejny skróci mi męki a raczej
nieudolne próby rozwiązania zadania.
25 sty 19:32
5-latek: Pani
Eta poszla na kisiel

25 sty 19:36
Tadeusz:
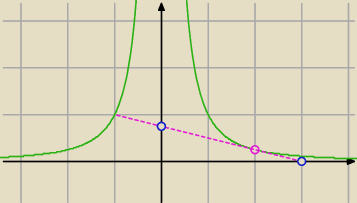
25 sty 19:40
Dżepetto 18: Tadeusz, czy mógłbyś przybliżyć mi rozwiązanie niegraficzne tego zadania? Wyczuwam pochodną.
Ew. Mogę jeszcze poczekać, może Eta niebawem zajrzy

| | 1 | | 1 | |
Ps. Z odpowiedzi wiem, ze takie punkty są dwa (−2, |
| ) lub (2, |
| ) |
| | 4 | | 4 | |
25 sty 19:50
Eta:

Taka właśnie mają być odp
25 sty 20:00
Eta:
| | 1 | | 2 | |
f(x)= |
| , x≠0 to f'(x)= − |
| |
| | x2 | | x3 | |
styczna ma równanie : y=ax+b w punkcie P(u, f(u)) ( zamiast x
o piszę u
| | 2 | | 1 | | 2 | | 3 | |
to a= f'(u)= = |
| i |
| = − |
| *u+b ⇒ b= |
| |
| | u2 | | u2 | | u2 | | u2 | |
A
oy(0,y) i B
ox(x,0) −−− punkty przecięcia stycznej z osiami
| | 3 | | −2 | | 3 | | 3 | |
to dla x=0 y= |
| , dla y=0 |
| *x+ |
| =0 ⇒ x= |
| u |
| | u2 | | u3 | | u2 | | 2 | |
| | 1 | | 3 | | 3 | | 9 | |
P(ΔABP)= |
| *| |
| |*| |
| u|= |
| |
| | 2 | | u2 | | 2 | | 8 | |
| | 1 | | 1 | |
to ............ |4u|=8 ⇒ u= 2 v u= −2 to f(2)= |
| v f(−2)= |
| |
| | 4 | | 4 | |
| | 1 | | 1 | |
styczną należy poprowadzić w punktach (2, |
| ) lub (−2, |
| ) |
| | 4 | | 4 | |

25 sty 20:11
Eta:
Pewnie
Dżepetto też poszedł na
kisiel 
25 sty 20:25
Tadeusz:
Funkcja jest parzysta zatem policzymy tylko jeden punkt
Zatem nasza styczna
| | 1 | | −2 | | −2x | | 3 | |
y− |
| = |
| (x−xc) ⇒ y= |
| + |
| |
| | xc2 | | xc3 | | xc3 | | xc2 | |
Teraz policz punkty przecięcia z osiami
dla y=0 ...itd
Z pola policzysz x
c
25 sty 20:29
Eta:

25 sty 20:30
Dżepetto 18: Eta wróciła!

| | 2 | | 2 | |
Mam już pytanko: a=f'(u) to oczywiste lecz dlaczego f'(u) = |
| skoro f'(x) = − |
| |
| | u2 | | x3 | |
?
25 sty 20:33
Eta:
Sorry ........to chochlik ....popraw

25 sty 20:35
Dżepetto 18: | | −2 | | 1 | | −2 | |
f'(u)= |
| i |
| = |
| u +b |
| | u3 | | u2 | | u3 | |
25 sty 20:38
Dżepetto 18: | | 1 | | 2 | |
i z tego wynika nam, ze b= |
| + |
| |
| | u2 | | u3 | |
25 sty 20:39
Dżepetto 18: Dalej mam liczyc już analogowo z poprawionym b?

25 sty 20:40
Eta:
| | −2 | | −2 | |
tylko ma być : |
| *u= |
| |
| | u3 | | u2 | |
25 sty 20:47
Eta:
| | 3 | |
b= |
| tak jak, podałam ........ |
| | u2 | |
25 sty 20:47
Dżepetto 18: ok, dziękuję za kolejna pomoc.
Miłego wieczoru
Eta!

25 sty 21:26
Eta:
Na zdrowie


25 sty 21:27





 Taka właśnie mają być odp
Taka właśnie mają być odp









