Wyznacz wszystkie wartości parametru m, dla których równanie x^3-3x+2=m ma dwa p Gabi: Proszę o pomoc w zadaniu Wyznacz wszystkie wartości parametru m, dla których równanie x³−3x+2=m ma dwa pierwiastki ujemne i jeden dodatni. Rozwiązałam równanie za pomocą schematu Hornera i wyszły mi 2 pierwiastki: x₁=1 ; x₂=1 ; x₃=−2 , a więc mam tylko 2 pierwiastki, z czego jeden jest dwukrotny, więc chyba nie jest to dobre rozwiązanie. Czy ktoś mógłby pomóc mi w rozwiązaniu tego zadania, abym otrzymała 2 pierwiastki ujemne i jeden dodatni?

pigor: ..., piszę online, a więc proszę wybaczyć ... język, może nie ... otóż, L=f(x)= x³−3x+2= x³−x−2x+2=x(x²−1)−2(x−1)= (x−1)(x²+x−2)= (x−1)(x−1)(x+2), czyli f(x)= (x−1)²(x+2) − funkcja lewej strony danego równania,. gdzie x=1 − pierwiastek dwukrotny i f(1)=0 minimum lokalne , a w punkcie (x,y)=(0,f(0))= (0,2) wykres funkcji f przecina oś OY , no to jeszcze tylko pochodna f ' (x)= 3x²−3=0 ⇔ x²−1=0 ⇔ x=±1 przy czym f(−1)= 4 − f_max, lokalne , a więc mam w ... głowie szkic wykresu dla potrzeb tego zadania z którego odczytuje , że prosta prawej strony równania f(x)=m, czyli prosta y =m przecina wykres funkcji f w 3−ech punktach: dwóch o odciętych ujemnych i jednym o odciętej dodatniej ⇔ 2< m< 4 ⇔ ⇔ m∊(2;4) − szukana odpowiedź spełniająca warunki zadania ...

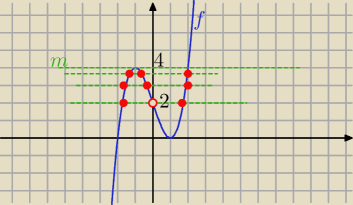Eta: 1/ narysuj wykres f(x)=x³−3x+2 2/ y=m dwa pierwiastki ujemne po lewej i jeden dodatni po prawej odp: m∊(4, 2)

pigor: ..., czeski błąd m∊(2;4) ...

Eta: Jasne jak

pigor: ..., to już ... drugi raz ; chyba ... zakochała się nam Pani η