proszę o rozwiązanie Michał: w trójkącie prostokątnym o przyprostokątnych a i b poprowadzono z wierzchołka kąta prostego

	h2		1		2ab
wysokość i dwusieczną. Wykaż że		=		* ( 1 +		)
	d2		2		a2 + b2

gdzie h jest długością wysokości , d − długością odcinka dwusiecznej zawartego w trójkącie nie wiem może trzeba lewą stronę przekształcić

Mila: Oblicz h i d.

Michał: po obliczeniu

	(a+b)2*d2
h = √
	2*(a2 +b2)

Mila: Skąd ten wynik? Z przekształcenia podanego wzoru czy z trójkąta?

tosia: przpepraaszam za wtrącenie . milu odpowiesz na moje pytanie pózniej ?

Michał: wynik jest po przekształcenia wzoru ale chyba nie tedy droga myślę ze trzeba z trojkata jak cos bede mial to napiszę

Michał: z korzystałem z tw o dwusiecznej kąta w trójkącie , oraz z tw o wysokości poprowadzonej z wierzchołka kąta prostego ale nic mi nie wychodzi musi być jeszcze jakieś tw

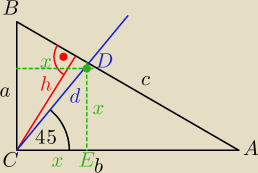
Mila: Proste związki w Δ prostokątnym. 1) c²=a²+b² c=√a²+b²

	1
PΔ=		a*b
	2

1		1
	a*b=		c*h⇔
2		2

ab=c*h

	ab
h=
	c

	a2*b2
h2=
	a2+b2

=================== 2) odcinek dwusiecznej: ΔDEA∼ΔBCA⇔

x		a
	=
b−x		b

	a*b
⇔x=
	a+b

d jest przekątna kwadratu o boku x

	a*b√2
d=
	a+b

	2a2b2
d2=
	(a+b)2

=================

h2		a2*b2		(a+b)2
	=		*		⇔
d2		a2+b2		2a2*b2

h2		a2+b2+2a*b
	=		=
d2		2(a2+b2

	1		ab
=		+		⇔
	2		a2+b2

h2		1		2ab
	=		*(1+		)
d2		2		a2+b2

============================== cnw

Michał: dziękuję bardzo