Wykres funkcji trygonometrycznej Kraterek: Naszkicuj wykres funkcji f(x) = cos2πx i rozwiąż nierówność f(x) ≥ 0

Bogdan:

Eve: cost≥0⇒cost≥cosπ⇒t≥π wracamy do 2πx

Kraterek: Bogdan, dzięki ale jak do tego dojść?

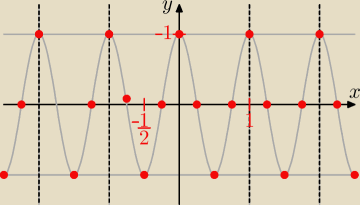
Bogdan: Okres funkcji g(x) = cosx jest równy 2π Wyznaczamy okres funkcji f(x) = cos(2πx): 2πx = 2π ⇒ x = 1, okres T = 1 Wyznaczamy argumenty funkcji, dla których f(x) = −1 oraz f(x) = 1

	1
cos(2πx) = −1 ⇒ 2πx = −π + k*2π ⇒ x = −		+ k, k∊C
	2

cos(2πx) = 1 ⇒ 2πx = k*2π ⇒ x = k, k∊C Wyznaczamy miejsca zerowe:

	π		1		1
f(x) = 0 ⇒ cos(2πx) = 0 ⇒ 2πx =		+ kπ ⇒ x =		+		k
	2		4		2

Zaznaczamy te punkty i łączymy zgrabnie cosinusową linią