planimetria, proste zadania maturalne, sprawdzenie rozwiązania Michał: Witam, Mam problem z zadaniem. Problem polega na tym, że znowu mój wynik nie zgadza mi się z wynikiem z odpowiedzi. Zadanie brzmi. Promień okręgu wpisanego w trójkąt prostokątny jest równy 200. Tangens jednego z jego kątów

	3
ostrych wynosi		. Oblicz odległość między wierzchołkiem kąta prostego a punktem
	4

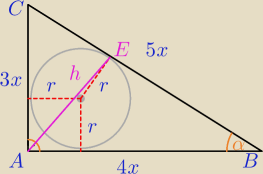
styczności okręgu z przeciwprostokątną. 1.Rysunek

	|AC|		3
tgα=		=
	|AB|		4

|BC|²=9x²+16x² |BC|=5x h=2r |CE|=3x−r=3x−200 |BE|=4x−r=4x−200 3x−200+4x−200=5x x=100

	1
P=300*400*		=60000
	2

	1
P=500*h*		=60000
	2

h=240 Tymczasem odpowiedź to 40√145 . Nie widzę swojego błędu, mógłby ktoś mi pomóc? Bardzo dziękuję

Michał: Dobra, chyba już widzę, co źle sobie założyłem. zaraz dam odpowiedź.

Michał: Skorzystałem z trójkąta AEC, uprzednio licząc CE=100 i cos kąta przy wierzchołku C, który wynosi 3/5 Z twierdzenia cosinusów policzyłem sobie bok AE, trójkąta AEC i otrzymałem 80√10 . Całkiem prawdopodbne, tym bardziej, że jest zbliżone do mojej wysokości, czyli 240, ale jednak nie jest to 40√145. Nadal nie wiem gdzie robię błąd. Dziękuję i z góry pozdrawiam

Mila: 1) |AE| − jest odległością punktu E od wierzchołka kąta prostego. AE nie jest prostopadłe do BC.

	3
2) tgα=		, α− kąt ostry
	4

	4
Z jedynki tryg. cosα=
	5

x=200 |AB|=800 |EB|=800−200=600

	4
|AE|2=8002+6002−2*600*800*
	5

|AE|²=232 000=100*2320=100*16*145 |AE|=4*10*√145

Mila: