proste zadanie z planimetri-sprawdzenie rozwiązania
Michał:
Witam,
Mam problem z zadaniem.Oto jego treść.
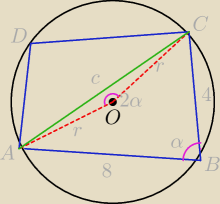
W okrąg o środku O wpisano czworokąt ABCD taki, że |AB|=8 i |BC|=4. Oblicz promień tego okręgu,
jeżeli kąt między promieniami AO i CO ma miarę 120.
Tak wygląda mój rysunek, moja interpretacja treści zadania,a rozwiązanie następująco.
Z tw. cosinusów.
2α=120 => α=60
c
2=64+16−64*cos60=64+16−32=48
c=4
√3
Znowu z twierdzenia cosinusów.
48=2r
2−2r
2cos120=2r
2+2r
2cos60=3r
2
16=r
2
r=4
| | 4√21 | |
To jest mój wynik, jednak w odpowiedziach jest podany dość dziwny, a mianowicie |
| |
| | 3 | |
Proszę Was o sprawdzenie rozwiązania i ewentualne pokazanie mi mojego błędu. Z góry dziękuję i
pozdrawiam! Michał
24 sty 14:15
Eve: c mam takie samo, ale w następnym tw się pomyliłeś
24 sty 14:29
Michał: A możesz mi powiedzieć, jak jest poprawnie, bo nie widzę błędu

24 sty 14:33
Eve: oki, moje niedopatrzenie, zastanawiał mnie ten 2r2, teraz widzę, że jest bobrze
mój promień też 4
24 sty 14:35
Michał: Jeszcze się zastanawiam, czy może autorowi chodziło o odwrotne określenie tego kąta, w sensie,
żeby to moje 2α=240, tylko nie wiem, czy to coś zmienia finalnie. W każdym razie, jeśli ktoś
znajdzie błąd to proszę o wskazanie.
24 sty 14:41
Eve: dokładnie tak, autorowi chodziło o ten drugi przypadek, i tam rzeczywiście jest tak jak w odp
24 sty 14:46
pigor: ..., wszystko formalnie gra, ale czy może
być jednocześnie |OC|=4 i |BC|=4

;
−−−−−−−−−−−−−−−−−−−−−
dany czworokąt istnieje gdy wszystkie jego 4
wierzchołki leżą po jednej stronie średnicy okręgu,
zrób więc nowy rysunek i ....

licz.
24 sty 14:52
Michał: Faktycznie, zgadza się. Ciekawe, czy w takim zadaniu na maturze, trzeba by rozważać obydwa
przypadki, czy tylko jeden. Bo nie ukrywam, nie zastanawiałbym się nad tym drugim
rozwiązaniem.
24 sty 14:55
Michał: @pigor
Skonstruowałem sobie na kartce dokładnie tą sytuację z tymi wymiarami i wychodzi na to, że jest
dobrze, tylko, muszę rozpatrzeć także drugi przypadek. Ten mój trochę nietypowy, faktycznie bo
jednym z boków czworokąta jest średnica okręgu na nim opisanego, ale możliwy.
24 sty 15:46
Michał:
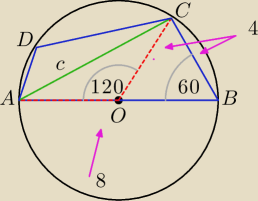
24 sty 15:54
pigor: ..., bardzo trafne spostrzeżenie; przypadek szczególny jest; tak trzymaj ...

24 sty 19:33
 Witam,
Mam problem z zadaniem.Oto jego treść.
W okrąg o środku O wpisano czworokąt ABCD taki, że |AB|=8 i |BC|=4. Oblicz promień tego okręgu,
jeżeli kąt między promieniami AO i CO ma miarę 120.
Tak wygląda mój rysunek, moja interpretacja treści zadania,a rozwiązanie następująco.
Z tw. cosinusów.
2α=120 => α=60
c2=64+16−64*cos60=64+16−32=48
c=4√3
Znowu z twierdzenia cosinusów.
48=2r2−2r2cos120=2r2+2r2cos60=3r2
16=r2
r=4
Witam,
Mam problem z zadaniem.Oto jego treść.
W okrąg o środku O wpisano czworokąt ABCD taki, że |AB|=8 i |BC|=4. Oblicz promień tego okręgu,
jeżeli kąt między promieniami AO i CO ma miarę 120.
Tak wygląda mój rysunek, moja interpretacja treści zadania,a rozwiązanie następująco.
Z tw. cosinusów.
2α=120 => α=60
c2=64+16−64*cos60=64+16−32=48
c=4√3
Znowu z twierdzenia cosinusów.
48=2r2−2r2cos120=2r2+2r2cos60=3r2
16=r2
r=4

 ;
−−−−−−−−−−−−−−−−−−−−−
dany czworokąt istnieje gdy wszystkie jego 4
wierzchołki leżą po jednej stronie średnicy okręgu,
zrób więc nowy rysunek i ....
;
−−−−−−−−−−−−−−−−−−−−−
dany czworokąt istnieje gdy wszystkie jego 4
wierzchołki leżą po jednej stronie średnicy okręgu,
zrób więc nowy rysunek i .... licz.
licz.

