nierówność john2:

3√x5 − 23√x4
	> 0
3√x9

(pod pierwiastkami w liczniku mamy x⁵ i x⁴, w mianowniku x⁹) Tak to powinno wyglądać? Dziedzina: x ≠ 0

3√x5 − 23√x4
	> 0 / * (3√x9)2
3√x9

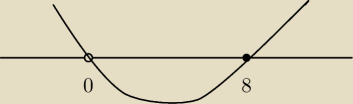
³√x⁹ * (³√x⁵ − 2³√x⁴) > 0 Szukam miejsc zerowych tych czynników ³√x⁹ = 0 ∨ ³√x⁵ − 2³√x⁴ = 0 x = 0 ∨ ³√x⁵ = 2³√x⁴ /³ x = 0 ∨ x⁵ = 8x⁴ x = 0 ∨ x⁵ − 8x⁴ = 0 x = 0 ∨ x⁴(x − 8) = 0 x = 0 ∨ x = 0 ∨ x = 8 zero jest pięciokrotnym pierwiastkiem (do dziedziny nie należy, ale rozumiem, że przy rysowaniu muszę je uwzględnić?), osiem pojedynczym Rysuję. Rozwiązanie x < 0 lub x > 8

Eve: zawsze musisz uwzględnić wszystkie pierwiastki, potem je eliminujesz jeśli trzeba

john2: Aha. Czyli Twoje rozwiązanie by wyglądało tak samo, jak moje?

Eve: nie by wyglądało, a wygląda tylko uważałabym w mnożeniu nierówności przez wyrażenie, którego znaku nie znam, skorzystaj

	a
raczej z tego, że		>0⇔a*b>0
	b

john2: Ok. Dziękuję. Tak w zasadzie zrobiłem tylko mniej bezpośrednio, (³√x⁹ )² jest ≥ 0