Rozwiąż rownanie i nierówność jaga05: błagam jeszcze te dwa przykłady, jak mam to zrobić ? 2Ix+1I −3=IxI −2Ix−5I +8<IxI

maria:

BiebrzaFun : jaga05dwojgaimionmario,zajrzyj tu,jest naprawdę wytłumaczone na babski rozum https://matematykaszkolna.pl/strona/1807.html

AROB: pomogę

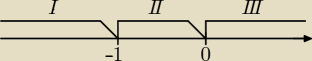AROB: zad. 1. 2Ix + 1I − 3 = IxI Miejsca zerowe: x = −1, x = 0 I. x ∊ (−∞, −1) x(−x −1) − 3 = −x −2x − 2 − 3 = −x −2x = 5 ⇒ x = 5 ∉ (−∞, −1) II. x ∊ <−1, 0) 2(x + 1) − 3 = −x 2x + 2 − 3 + x = 0

	1
3x = 1 ⇒ x =		∉ <−1, 0)
	3

III. x ∊ <0, ∞) 2(x + 1) − 3 = x 2x + 2 − 3 − x = 0 ⇒ x = 1 ∊ <1, ∞) Odp. x = 1

Łukasz: I. x=−5 ∊(−∞,−1) II. tu jest dobrze III wynik jest dobry tylko przedział powinien być taki <0,+∞) odp.x=1 ∨ x=−5

AROB: Dzięki Łukaszu, masz rację. Tak to jest, gdy jednym okiem ogląda się TV.

AROB: piszę zad, 2.

AROB: Zad. 2. −2Ix − 5I − 8 < IxI Miejsca zerowe: x = 5, x = 0. I. x ∊ ( −∞, 0) −2(−x+5) − 8 < −x 2x − 10 −8 +x < 0 3x < 18 / : 3 x < 6 ∧ x ∊ (−∞, 0) ⇔ x ∊ (−∞, 0) II. x ∊ <0, 5) −2(−x + 5) − 8 < x 2x − 10 − 8 < x x < 18 ∧ x ∊ <0, 5) ⇔ x ∊ <5, ∞) III. x ∊ < 5, ∞) −2( x − 5) − 8 < x −2x + 10 − 8 < x −3x < −2 / : (−3)

	2
x >		∧ x ∊ <5, ∞) ⇔ x ∊ <5, ∞)
	3

Po dodaniu 3 przedziałów otrzymujemy rozwiązanie: x ∊ R