Bok AB prostokąta ABCD ma długość 4√3, a przekątna AC tworzy z bokiem BC kąt o m
Anka: Bok AB prostokąta ABCD ma długość 4√3, a przekątna AC tworzy z bokiem BC kąt o mierze 60
stopni. NA BOKACH PROSTOKĄTA ABCD WYBRANO PUNKTY E i F w taki sposób, że punkt E należy do
boku AB, a punkt F − do boku CD, a czworokąt AECF jest rombem. Oblicz pole tego rombu.
23 sty 22:43
Anka: proszę o pomoc
23 sty 22:53
Eta:
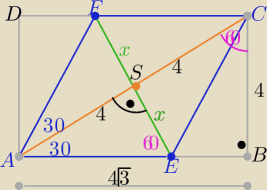
|AC|=8 , |BC|=4 , |AB|=4
√3
x=........... , |EF|=2x=......
| | |AC|*|EF| | |
P(rombu)= |
| =......... |
| | 2 | |
23 sty 23:27
Eta:
Można też tak:
Prostokąt składa się z sześciu przystających trójkątów prostokątnych
Romb składa się z czterech takich trójkątów
| | 4 | | 2 | | 2 | |
to P(rombu)= |
| = |
| P(prostokąta) = |
| *4*4√3= ...... |
| | 6 | | 3 | | 3 | |
23 sty 23:35
pigor: ..., niech x − długość boku rombu, to
z warunków zadania i własności rombu: masz
| | 4√3−x | | 1 | |
np. z ΔEBC : |
| = cos60o=sin30o = |
| ⇒ |
| | x | | 2 | |
⇒ x = 8
√3−2x ⇔ 3x = 8
√3 ⇔ x=
83√3 , zatem
PACEF= x
2sin60
o =
643*
12√3=
323√3 . ...
23 sty 23:35
Eta:
23 sty 23:36
Anka: a skąd znamy tą 4?
23 sty 23:41
Eta:
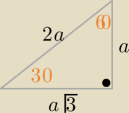
23 sty 23:46
anka: dziękuję
23 sty 23:49
Eta:
23 sty 23:50