średnio trudne zadanie z geometrii analitycznej Maciek: Punkty A(2,−3) i B(5,1) są wierzchołkami trójkąta ABC. Bok BC zawiera się w prostej k: x+2y−7=0, zaś środkowa Am zawiera się w prostej m: 5x−y−13=0. Wyznacz równanie ogólne prostej, w której zawiera się wysokość trójkąta poprowadzonego z wierzchołka C. Wychodzi mi 3x+4y−17=0, a w odpowiedziach jest 3x+4y−15=0 nie mogę znaleźć błędu proszę o pomoc!

Tadeusz:

	1+3		4
Prosta przez punkty A i B ma współczynnik kierunkowy a=		=
	5−2		3

Wysokość poprowadzona z C

	3
y−3=−		(x−1)
	4

4y−12=−3x+3 ⇒ 3x+4y−15=0

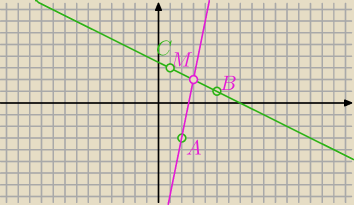
Madi: najpierw musisz wyzanczyc współrzędne M z układu rownań prostej m i k (wychodzi M(3,2)). Potem wyznaczasz rownanie prostej AB, AB: −3y+4x−17=0. Prawdopodobnie obliczyles rownanie prostej AB zamiast wysokości trójkąta . Prosta w ktorej zawiera sie wysokosc poprowadzona z C jest taka że pr AB⊥ pr C, więc jej równanie to C: 3x+4y+L=0. Teraz podstawiasz wspołrzędne punktu C i otrzymujesz ze L=−15. Równanie prostej C: 3x+4y−15=0

Tadeusz: Madi ... na takich współrzędnych punktu M na pewno nie wyjdzie

Madi: mi wyszło i to dobrze spradziłam w geogebrze

Madi: w odpowiedziach jest tez tak samo