Pomozcie kochani :) Ania: Wyznaczyc funkcje f o g dla f(x)=lnx i g(x)=−x² +6x−5 Podać jej dziedzinę i zbio wartosci.

Eve: f◯g=f(g(x))

Ania: No tak ale pozniej jak z pochodnej wyznaczyc dziedzine i zbior wartosci..? :<

Eve: napisz mi to złożenie

Ania: f(x)=ln(−x²+6x−5)

5-latek: Tez chetnie zobacze gdyz sam nieraz mam z tym trudnosci

Ania: lnx=1/x czyli ln1/−x2+6x−5

5-latek: Wydaje mi sie ze tutaj nie ma potrzeby korzystania z pochodnej . Tylko z definicji logarytmu wyznaczyc dziedzine liczby logarytmowanej

Eve: no to jakiej liczby nie może być w nawiasie?

Eve: albo jaka musi być?

Ania: Ja to nie mam pojecia, jakbym wiedziala to bym tutaj nie pisala

Eve: lnx=y⇒e^y=x, jaki jest x? to chyba wiesz?

polaczek: Policz delte i tyle

Eve: jesteś Ania?

Eve: dobra, wrócę za pół godz, dokończymy

polaczek: Jestem, nie wiem jak się do tego zabrać.

5-latek: Przepraszam CIe bardzo Eve Ale to nie jest w Twoim interesie wracac ,tylko w intersie naszej panny . Niech sama poprosi o pomoc jak wroci

Eve: e jest dodatnia, to jaka jest jej potega?

5-latek: Eve Na randki chyba tez chodzilas punktualnie

Eve: tak juz mam, nie spóźniam sie nigdy i nigdzie

Eve: zrezygnowałeś? nieładnie

Ania: Oki jestem

Eve: 18.58 odpowiedz

Ania: dodatnia

Eve: i jestesmy na dobrym kursie −x²+6x−5>0 znajdź pierwiastki

Ania: x1=5 x2=1

Eve: dobrze, teraz narysuj wykres i podaj przedział gdzie to jest >0

Ania: w przedziale od <1,5>

5-latek:

Eve: otwarty (1,5) teraz wartości funkcji g(x), czyli trzeba znaleźć wierzchołek paraboli

Ania: W= (3,4)

Eve: ok, czyli Z_w[g(x)]=(3,4>

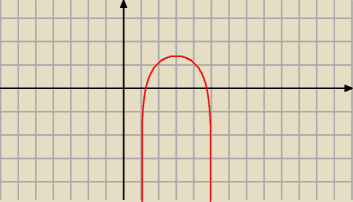
5-latek: Ja tez sie ucze na tym zadaniu . Jak narysowalem sobie wykresy funkcji w tym programie to wyszly inne zbiory wartosci dla obu tych funkcji np wykres funkcji y=ln(−x²+6x−5 ) Wiec wcale nie wyjdzie ten sam co y=−x²+6x−5 . Dlaczego ?

Eve: błąd Z_w[g(x)](0,4> teraz wartości f(g(x)) powinniśmy policzyć pochodną, przyrównać do zera, policzyć wartości na końcach przedziału i dla piewrwiastków pochodnej,że by znaleźć największą i najmniejszą wartość ale na wszelkie sposoby wychodzi min dla ln0=−∞ i max ln4

Eve: 5−latku wartości obu nie są takie same, masz wartości f(g(x))

Ania: Dobra poddaje się, zajmę się lepiej ćwiczeniem przykładów z pochodnych. Dziękuje, trzymajcie sie

Ania: Tzn. poddaje się w tm zadaniu tylko. Może wiecię jak to popchnąć dalej? an=ⁿ√√2n + 4n + n2 Moim zdaniem tutaj trzeba skorzystać z twierdzenia o trzech ciągach, ale zawsze wszystkie liczby pod pierwiastkiem były podniesione do potęgi "n" a teraz jedna jest do "2" no i niewiem :<

Eve: masz rozwiązanie i przykro mi, że nawet nie spojrzałaś

Eve: było dziś, n²<4ⁿ

5-latek: Eve Moze jak zaczne pochodne za rok to mi pokazesz jak to sie liczy dokladnie Proste pochodne umiem policzyc.

Eve: nie ma sprawy

Ania: Spojrzałam, ale i tak mi nic to nie rozjaśniło więc narazie bedę się uczyć z pochodnych, te zadanie zostawie na koniec jak wystarczy czasu. n²<ⁿ√2n + 4n + n2<4ⁿ Tak rozumiem to co napisałaś i teraz dolna i górna granica musi się równać tyle samo żeby ten ciąg równał sie tyle co górna i dolna tak?

Eve: hej, hej ale to zadanie z funkcjami mamy skończone

Ania: Wiem, ale tego nie rozumiem, i nie bede przy tym siedziała kolejnej godziny bo czasu coraz mniej

Ania: Więc postanowiłam zostawic to na koniec

Eve: aha, no to koniec

Ania: No tak ale jeszcze mam pytanie odnośnie tego ciągu, jestes jeszcze?