aksjomat Blue: Mam problem z trzema zadaniami: zad.1 Rzucamy dwa razy symetryczną monetą i dwa razy sześcienną kostką. Oblicz prawdopodobieństwo tego, że moneta upadnie za każdym razem tą samą stroną, pod warunkiem, że na kostce wypadnie dwa razy parzysta liczba oczek. Zakoduj wynik podając trzy początkowe cyfry po przecinku jego rozwinięcia dziesiętnego. Mi wyszło 125, a w odpowiedzi mam 500. zad. 2 Miary α, β, γ kątów wewnętrznych trójkąta spełniają warunek sinα= 2sinβcosγ. Udowodnij, że ten trójkąt jest równoramienny. zad.3 Jaki powinien być kąt przy wierzchołku trójkąta równoramiennego o danym polu, aby promień okręgu wpisanego w ten trójkąt był największy? eeee.... problem w tym, że nie podali, żadnego pola, więc nie wiem, o co chodzi w tym zadaniu... xd Pomocy

wmboczek: 1. Kostka do monety ma się nijak − zdarzenia niezależne, można rozważać tylko monety

wmboczek: 2. α=180−β−γ sinα=sin(β+γ)= wzór = na jedną stronę i ten sam wzór sin(β−γ)=0 no i mamy

Blue: Czyli w tym 2 udowodniłeś, że β=γ tak?

Kacper:

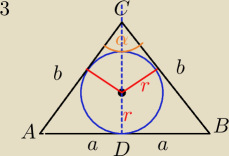
Mila: Zadanie 3. P− pole ΔABC |AB|=2a

	1		√2P *sinα
P=		b2sinα⇔b=
	2		sinα

W ΔCDB:

	α		a		α
sin		=		⇔a=b*sin		⇔
	2		b		2

	√2P* sinα		α		√2P*sinα
a=		*sin		⇔a=
	sinα		2		α   2 cos   2

P=(a+b)*r⇔

	√2P*sinα		√2P *sinα
P=(		+		)*r⇔
	α   2 cos   2		sinα

	1		1
P=√2P*sinα*(		+		)*r⇔
	sinα		α   2cos   2

	α   1+sin   2
P=√2P*sinα*		*r⇔
	α   α   2 sin *cos   2   2

	α   √2P*sinα*(1+sin )   2
P=		*r⇔
	sinα

	√2P		√sinα
r(α)=		*
	2		α   1+sin   2

Teraz oblicz r'(α)

	π
Funkcja r(α) osiąga maksimum dla α=
	3

===============================

Blue: dzięki

Kacper: Sporo zachodu

Blue: Mila, na pewno nie ma prostszego rozwiązania do tego 3 zadanka?

Mila: Nie ma specjalnej drogi dla Blue.

Blue: Mila, ale czy nie sądzisz, że to zadanko jest trochę za trudne jak na maturalne?

Mila: Owszem, za trudne, ale ćwiczysz umysł, biegłość rachunkową.