styczna do funkcji dragon: Dana jest funkcja

	x−2
f(x)=
	x−5

Uzasadnij ze kąt między styczną do wykresu a osią OX jest kątem rozwartym oraz znajdź równanie stycznej, dla której kąt między styczną do wykresu a osią OX jest równy 135 stopni

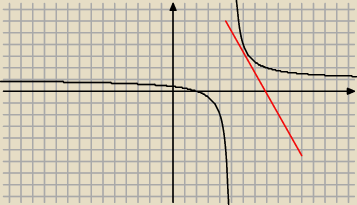
dragon: Tak w sumie nie wiem od czego zacząć, bo to jest funkcja homograficzna. narysowałem tylko w sumie wykres z którego widac że styczna musi być malejąca, co wskazuje że tworzy z osią OX kąt rozwarty... ale jak to opisać? a co do drugiej częsci zadania to nie mam żadnego pomysłu.

Frost:

x−2		x−5+3		3
	=		=1+
x−5		x−5		x−5

	3		x−2
y=		Translacja o wektor [5,1] f(x)=
	x		x−5

Nie wiem czy można z rysunku ale pewnie można, to widać. a potem ten kąt 135^o : tg135^o=a y=ax+b masz a z tg brakuje Ci b. Jak możesz porównać wzór prostej y i f(x) będziesz miał punkty styczności

dragon:

	−√2
tzn wiem, że tg135 to będzie		I to posłuży przy wzorze na równanie stycznej. ale
	2

skąd mam wziąć x₀

dragon: O, super kolego Frost, o to mi chodziło

dragon: aczkolwiek nie do końca, bo tu chyba trzeba użyć również pochodnej prawda?

Frost: Możesz i z pochodnej y−f(x₀)=f'(x₀)(x−x₀) gdzie: f'(x₀)=a

5-latek:

	−√2
Ale rowniez tg135≠		tylko =−1
	2

Frost: tg(135^o)=tg(90^o+45^o)=−ctg(45^o)=−1

dragon: lekka kaszanka mi wychodzi... jak wam wychodzi to b?

dragon: bo sprowadziłem

x−2−(−x+b)(x−5)
	=0
x−5

x2−x(4+b)+5b−2
	=0
x−5

i wychodzi mi Δb=226...

dragon: A NIE, dobra, już wiem Δb=48 mi wychodzi...

dragon: ok, już wybrnąłem, super dzięki za pomoc,Frost

Frost: Rozumiem, że z pochodnej nie robisz?