równania bajabongo: Rozwiąż równianie: √2+√2+√x=4 muszę to podnieść do kwadratu i do kwadratu i później do kwadratu czy jak?

Eve: niestety tak i nie zapominaj wymiernych wyrażen przenosić

3Silnia&6: przenies √2 na prawo i odustronie podniesc do kwadratu 2 razy.

bajabongo: tak tylko że ten √2 na początku odnosi się do całego wyrażenia... i wychodzi mi x=100 jak tak to wyliczę..

PW: A gdy podstawisz x = 100 do zadanego równania, to otrzymasz zdanie prawdziwe?

majo: nie..

bajabongo: no nie, pewnie że nie wyjdzie

bajabongo: to będzie 4 tylko jak to wyliczyć?

bajabongo: kurde, pomyliłem cyfrę jedną... tam powinno być √2+√2+√x = 2

3Silnia&6: /² , x > 0 2 +√2+√x = 4 √2+√x = 2 /² 2 + √x = 4 √x = 2 /² x = 4

bajabongo: dziękuję, i sorry za moją głupotę.. rzeczywiście jak tak się patrzy to wydaje się to zadanie nawet łatwe..

bajabongo: a jeżeli mam np. x⁴−10x²+9=0 to muszę wyciągnąć przed nawias x² ? dobrze myślę?

3Silnia&6: podstaw za x² zmienna pomocnicza t x² = t, t >0 ( bo x² przyjmuje wartosci od 0 do niesk. ,dlatego t > 0) t² − 10t + 9 = 0 delta i te sprawy.

PW: To nic nie da. Jest to tzw. równanie "dwukwadratowe", gdy podstawimy x² = t ≥ 0, to stanie się jasność.

bajabongo: a pomożesz mi jeszcze z tym?..

	log(x2−11x+19)
jeżeli mam		= 2
	log(x+2)

to co muszę najpierw zrobić?

bajabongo: tak, podstawiłem i wyszło mi

bajabongo: ale co z tymi logarytmami zrobić?

3Silnia&6: 1* Dziedzina 2* obustronnie mnożysz przez (log(x+2))² log(x² −11x + 19) = 2log(x+2) = log(x+2)² = log(x² + 4x +4) [f. jest roznowartosciowa, wiec log(x² −11x + 19) = log(x² + 4x +4) ⇔ x² −11x + 19 = x² + 4x +4] x² −11x + 19 = x² + 4x +4 15 = 15x, x =1 spr. czy nalezy do dziedziny.

PW: W szkole mówią: − Najpierw określ dziedzinę D. Trzeba więc zadbać, aby x+2 > 0 i log(x+2) ≠ 0 i x² − 11x + 19 > 0. Gdy podasz D − pomyślimy dalej.

bajabongo: tak x=1 należy do dziedziny a jeżeli chodzi o określenie dziedziny to: x+2>0 x>−2 x²−11x+19>0 tutaj wychodzi mi 3√5 a log(x+2)≠0 to będzie 10^x=x+2 ?

3Silnia&6: log(x+2)=0 ⇔ x+2 = 10⁰ = 1, x = −1

bajabongo: a czy jak określam dziedzinę to też muszę liczyć to x²−11x+19>0 ? tam wychodzą liczby z pierwiastkiem..

3Silnia&6: musisz, pierwiastek oszacuj i wrzuc na os razem z innymi przedzialmi/pierwiastkami i odczytaj rozwiazanie.

bajabongo: nie wychodzi mi..... masakra jakaś.

3Silnia&6:

	11 + 3√5		11 − 3√5
√Δ = 3√5, x1 =		, x2 =
	2		2

felicita: tak, tak mi wyszło i zaokrągliłem wyniki do x₁=9 i x₂=2 ale jak mam to na osi zaznaczyć?

bajabongo: no ja też, mi tak wyszło ale nie wiem jak mam teraz tą dziedzinę określić... to ty też masz takie zadanie?

felicita: też... ale zostawiłem to rozwiązanie bo nie umiem tych logarytmów obliczać, tzn podstawy tak, ale nic poza..

3Silnia&6:

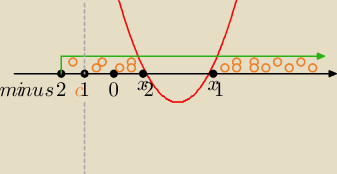
	11 − 3√5		11+3√5
x2 − 11x + 19 > 0 ⇔ x ∊ (−∞,		) U (		,∞ )
	2		2

−czerwony x + 2 > 0 ⇔ x > −2 − zielony log(x+2) = 0 dla x = −1 ( na osi zaznaczylem jako 1,bo nie moge znaku − dodac ) − szary czesc wspolna − pomaranczowy kolor = dziedzina

bajabongo: czyli dziedzina to będzie: D:<−2, 2>∪<x₁,+∞) tak? tak mogę to zapisac?

3Silnia&6:

	11−3√5		11+3√5
D: (−2,		) U (		,∞)
	2		2

3Silnia&6: Poprawka:

	11−3√5		3√5 + 11
D: (−2,−1) U ( −1		) U(		,∞)
	2		2

3Silnia&6: i nie bedzie D: (przedzialy) tylko D = (przedzialy )

bajabongo: ale to przy wszystkich tych liczbach jest nawias otwarty? nie ma przy− 1 domkniętego? przecież

	11−3√5
należy i te punkty		też.. czy nie?
	2

3Silnia&6: przy zalozeniach mamy nierownosci ostre ( tak wiec otwarte ) − na rysunku nie jest to zaznaczone.

3Silnia&6: i jak mozemy domykac przedzial przy 1, skoro naszym celem byla ja wyrzucic z dziedziny

3Silnia&6: −1*

bajabongo: A tak rzeczywiście, źle spojrzałem. Ok, czyli x=1 należy. dzięki za pomoc 3Silnia&6 !