Kombinatoryka Adrian: W loterii jest 10 losów, wśród których jest 6 losów pustych. Losujemy dwa losy. Prawdopodobieństwo wylosowania co najmniej jednego losu, który nie jest pusty, jest równe. Jest ktoś wstanie to jak najbardziej szczegółowo rozwiązać ? Wiem, że należy skorzystać z symbolu Newtona, dlaczego ?

Adrian: ?

Mila: 10 − liczba losów 6P,4W Losujemy 2 losy:

	10 2		1
|Ω|=		=		*10*9=45
			2

A− wylosujemy co najmniej jeden los wygrywający A' − wylosujemy dwa losy puste ( zdarzenie przeciwne)

	6 2		1
|A'|=		=		*6*5=15
			2

	15		1
P(A')=		=
	45		3

	1		2
P(A)=1−		=
	3		3

Można inaczej np.za pomocą drzewka.

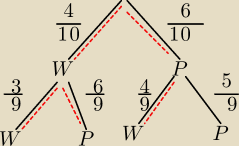
Mila: II sposób Sumujemy z tych ścieżek, gdzie jest los W.

	4		3		4		6		6		4		60		2
P(A)=		*		+		*		+		*		=		=
	10		9		10		9		10		9		90		3

Albo liczymy prawd. − tylko 2 losy P i odejmujemy od 1.

	6		5		30		1
P(A')=		*		=		=
	10		9		90		3

	2
P(A)=
	3

Adrian: A jak to zrobić pierwszym sposobem tylko zamiast A' od razu dać A, gdyż kompletnie nie ogarniam tego symbolu Newtona...

Mila: Co najmniej jeden los wygrywający⇔Jeden los W i jeden P lub dwa losy wygrywające.

	4 1		6 1		4 2
|A|=		*		+		=24+6=30

	30		2
P(A)=		=
	45		3

Adrian: Mam problem z jeszcze jednym zadaniem : Z ośmioosobowej grupy uczniów, wśród których są Adam i Beata, wybieramy losowo dwie osoby : a) Określ zbiór zdarzeń elementarnych dla tego doświadczenia b) Oblicz prawdopodobieństwo, że wybrano Adama i Beatę

	8 2
a )		? = 28

	8 1		8 1
b) |A| =		*		?

Adrian: b) nie jest możliwy nie przemyślałem tego.

Mila:

	1
b)		na jeden sposób możesz wybrać tę parę z 28 par.
	28

Adrian: Dziękuję pewnie jeszcze napisze.

xyz: Rzucono dwa razy symetryczna, sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia : A − suma wyrzuconych oczek jest liczba pierwszą B − iloczyn wyrzuconych oczek jest liczbą podzielną przez 3 C − za pierwszym razem wyrzucono liczbę nie wiekszą niż za drugim razem Jak obliczyć to zdarzenie elementarne ?

62 2		12 2
	czy

xyz:

	36 2
albo		?

nizirko: Денис лох