przebieg zmienności funkcji. Marta96:

	1		x
Witam. Mam problem z narysowaniem funkcji y=		i y=e[		]
	lnx		x−1

	1
funkcja
	lnx

1.dziedzina x>1 2.granice x−>1+ f(x)=+∞ x−>+∞f(x)=0 3.asymptoty x=1 asymptota pionowa obustronna y=0 asymptota pozioma obustronna brak asymptot ukośnych 4. ekstrema, monotoniczność dziedzina pochodnej xe(0,1)u(1,+∞) funkcja malejąca w dziedzinie, brak ekstremów 5.wypukłość, wklęsłość, punkty przebicia y''>0 dla xe (0,1/e²)u(1,+∞) y''<0 dla xe(1/e²,1) 6. tabelka w wierszu "x" uwzględniam tylko dziedzinę pierwszej funkcji, nie żadnych pochodnych? 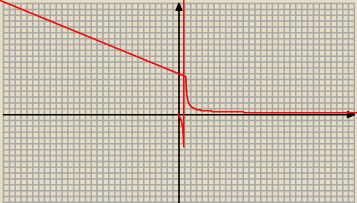jeżeli tak to mam 1,...,+∞ w 1 mam asymptotę i wykres wygląda jak hiperobola z prawej strony, po lewej stronie asymptoty nic nie rysuję?

	x
y=e[		]
	x−1

1.dziedzina x≠1 2.granice na krańcach dziedziny limx−>−∞f(x)=e limx−>1+f(x)=∞ limx−>1−f(x)=0 limx−>+∞=e 3.asymptoty x=1 asymptota pionowa lewostronna y=e asymptota pozioma obustronna 4. ekstrema, monotoniczność funkcja malejąca w dziedzinie tej samej co funkcja pierwotna brak ekstremów 5. wypukłość, wklęsłość, punkty przebicia

	1
y''>0 dla xe (		,1)
	2

	1
y''<0 dla xe(−∞,		)u(1,+∞)
	2

6. tabelka

	1
w wierszu "x" mam −∞,...,		,...1,....+∞
	2

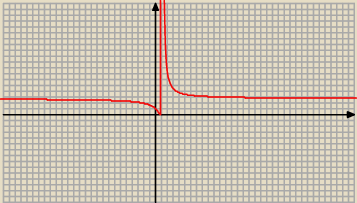
tutaj kompletnie nie wiem jak narysować ten wykres...

Janek191:

	1
y =
	ln x

Wykres funkcji ale bez tej skośnej półprostej ( coś się zniekształcił )

Janek191: