czy to zadanie jest błędne Michał: Podstawą ostrosłupa jest trójkąt prostakątny równoramienny o przyprostokątnych długości a Wszystkie jego krawędzie boczne mają długość 2a Ostrosłup ten przecięto płaszczyzną przechodzącą przez przeciwprostokątną podstawy i środek krawędzi bocznej przeciwległej do przeciwprostokątnej Oblicz sinα*cosα gdzie α jest miarą kąta nachylenia otrzymanego przekroju do podstawy ostrosłupa

	√7
wynik to
	8

ja robiłem to zadanie ale nie otrzymałem takiego wyniku proszę o rozwiązanie zadanie to już pisałem ale nikt nie udzielił odpowiedzi

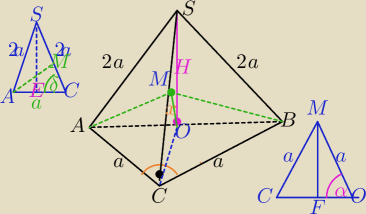
Mila: Wszystkie krawędzie boczne są równe⇔spodek wyskości ostrosłupa leży w środku okręgu opisanego na podstawie. W podstawie jest Δrostokątny, to środek okręgu opisanego leży w środku przeciwprostokątnej. |AB|=a√2

	a√2
|AO|=|OB|=|OC|=R =
	2

ΔABM− przekrój. ∡MOC=α |MC|=a

	1   a 2		1
W ΔACE: cosδ=		=
	2a		4

W ΔACM z tw. cosinusów:

	1
AM2=a2+a2−2*a*a *
	4

	1
AM2=2a2−		a2
	2

	3
|AM|2=		a2
	2

	√6
|AM|=		a
	2

============= W ΔAOM: |AM|²=|AO|²+|OM|²

	√6		√2a
(		a)2=(		)2+x2⇔x=a
	2		2

W ΔMOC:∡MOC=α,

	a√2
|OC|=
	2

	a√2
|OF|=
	4

	a√2   4		√2
cosα=		=
	a		4

sin²α+cos²α=1

	√2
sin2α=1−(		)2
	4

	1
sin2α=1−
	8

	7
sin2α=
	8

	√7
sinα=
	2√2

	√7		√2
sinα* cosα=		*		⇔
	2√2		4

	√7
sinα* cosα=
	8

===============

Michał: Mila jesteś wielka i dziękuję bardzo patrząc na twój rysunek to jest wszystko jasne mój problem polegał na tym że nie mogłem obliczyć wysokości Δ ABM ale jeszcze mam pytanie czy zamiast ΔACE nie ma być ΔECS to cosδ = ...

Mila: Tak, nie widać rysunku, gdy się pisze długi tekst, a może palec się źle ustawił na klawiaturze.

Michał: ja wiem że tak jest ale zawsze analizuję zadanie mimo że zostanie przez kogoś rozwiązane jeszcze raz dziękuję

Mila: To dobrze, że nie przepisujesz bezkrytycznie. Powodzenia w romansach z królową nauk.