granica ciągu artek: lim n→∞ arcctg(n−n²)

ICSP:

	π
−
	2

artek: jak to rozwiązałeś? jaką metodą?

ICSP: Ile wynosi lim_n→∞ (n − n²)

artek: −∞ ?

Gray: arcctg≠arctg

artek: lim n→∞ (n−n²) lim n→∞ n²(1/n−1) szacuję [∞*(0−1)] [−∞]

ICSP: widziałem jedno c Przepraszam Jednak sam sposób dojścia do wyniku się nie zmienia. lim_n (n − n²) = − ∞ ,

	π
limn arcctg(n − n2) = [arcctg(−∞)] =
	2

Co odczytujemy np z wykresu funkcji arcctg

ICSP: Gray pomógłbyś mi z jednym zagadnieniem ?

Gray: Tak. Ale przyznaj, że pomyliłeś się o 19:33

ICSP: Przyznaje pomyliłem się (Zresztą identycznie jak na kolokwium ostatnim)

Gray: Powinno być: arcctg(n−n²) → π (n→+∞)

ICSP: Nie wierze Wszystko co tutaj zrobiłem jest źle

Gray: Ludzką rzeczą jest błądzić; diabelską tkwić w błędzie...

Gray: Z jakim zagadnieniem miałbym Ci pomóc?

artek: napisze ktoś całe zadanie dobrze rozwiązane..? bo ja już się pogubiłem

ICSP: Interesuje mnie wyznaczenie elementów odwrotnych w Z[√3] = { a + √3b , a,b ∊Z} Dochodzę do momentu : (a + b√3)(c + d√3) = 1 i nie mogę ruszyć dalej. Nie mogę znaleźć odpowiedniej normy

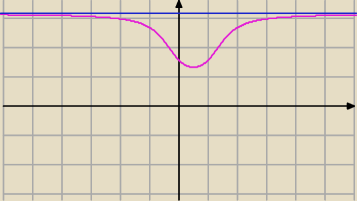
Gray: Napisałem o 20:40. Na rysunku funkcja arcctg(x−x²) − różowe, oraz jej asymptota y=π. Chyba wszystko jasne.

Gray: Jakiej normy? Wymnóż wszystko jak wielomian przez wielomian i zapisz w postaci: a+b√3, gdzie a,b∊Z. Otrzymasz układ równań do rozwiązania.

ICSP: ac + 3bd + (ad + bc)√3 = 1 skąd: ac + 3bd = 1 ad + bc = 0 i tutaj stoję

Gray: Dobrze. Rozwiąż ten układ np. ze względu na a,b. Ja zastosowałbym metodę wyznaczników.

ICSP: W = c² − 3d² W_a = c W_b = d

	c
a =
	c2 − 3d2

	d
b =
	c2 − 3d2

Co dalej ?

Gray: Dobrze. Teraz najtrudniejsze: kiedy (dla jakich c,d∊Z) a i b są całkowite?

ICSP: Czyli musi być : c² − 3d² | c ∧ c² − 3d² | d , ale niestety nie widzę nic więcej

Gray: Widać, że te warunki będą spełnione tylko dla wybranych c i d. Trzeba je spróbować jakoś wyznaczyć. (c,d) ∊ {(1,0), (−1,0)} jest OK. Coś jeszcze?

ICSP: Wymyśliłem coś takiego: Na pewno koniunkcja będzie spełniona gdy c² − 3d² = 1 bądź c² − 3d² = −1 Z pierwszej równości bardzo łatwo dostać c + √3d = ±(2 + √3)ⁿ , n ∊Z Druga jest z kolei sprzeczna bo patrząc na nią mod3 dostajemy : c² ≡ 2 mod 3 ale z symbolu Legendre'a :

2 3
	≡ 2(3 −1)/2 ≡ 2 ≡ −1 mod 3

Jednak mogą być jeszcze inne rozwiązania gdy c² − 3d² ≥ 2 i tutaj już kompletnie nie mam pomysłu, jak to dalej ruszyć

Gray: Mam robotę na jutro; muszę niestety skończyć na dziś, ale będę miał na uwadze to zadanie. Na razie nie widzę ładnego zakończenia.

ICSP: Dziękuję