Geometria- zadanie pulikowski: W trapezie równoramiennym ramiona mają długość 15. Przekątne trapezu są prostopadłe do ramion i mają długość 20. Wyznacz pole trapezu.

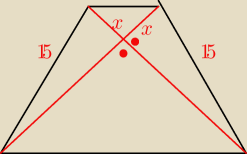
Janek191: Mamy x² + ( 20 − x)² = 15² x² + 400 − 40 x + x² = 225 2 x² − 40 x + 175 = 0 Δ = 1 600 − 4*2*175 = 1 600 − 1 400 = 200 = 100*2 √Δ = 10 √2

	40 − 10√2
x =		= 10 − 2,5 √2 lub x = 10 + 2,5√2
	4

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− zatem pole trapezu jest równe P = 0,5 x² + 0,5 ( 20 − x)² + x*( 20 − x) = ...

Janek191: Źle zrobiłem − przekątne miały być prostopadłe do ramion

Pudel i Piotruś: To się popraw:

	(a+b)h
P=
	2

a=25,b=7,h=12 Teraz jest klawo!

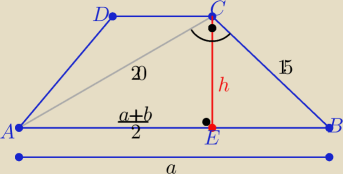
Eta: a=√400+225= 25 25*h=20*15 ⇒ h=12

a+b
	=√400−144=16
2

	a+b
P=		*h=16*12= 192[j2]
	2