Eta:
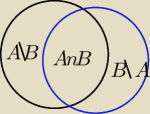
Zalezności między działaniami na zbiorach najlepiej widać na
schemacie Vena
tak więc:
A U B = (A \ B) U ( B \ A) U ( A∩ B)
to:
P( AUB) = P(A \B) + P(B \ A) + P(A∩B)
oraz : A∩B
' = A \ B i B ∩A
/ = B \ A
więc P(A∩B
') = P(A \B) i P(B∩A
')= P(B \A)
z treści zad. mamy ,że P(A∩B
') = P(B∩A
') => P(A\B)= p(B\A)
wracając do:
P(AUB) = P(A\B) +P(A\B) + P(A∩B)
to: 0,75 = 2P(A\B) +0,25 => 2P(A\B) = 0,5 => P(A\B) = 0,25
P(A\B) = 0,25
teraz podobnie zauważysz ,że: B= (B\A) U ( A∩B)
więc P(B) = P(B\A) + P(A∩B)
P(B) = 0,25 + 0,25 = 0,5
P(B)= 0,5