Figury geometryczne nr 3.
5-latek:
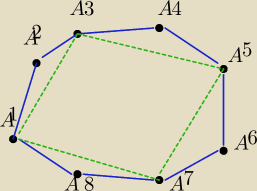
Uzasadnij (nie piszse udowodnij jak w innych zadaniach) poslugujac sie warunkiem trojkata ze
dlugosc dowolnej lamanej A
1, A
2.....A
n jest wieksza niz dlugosc odcinka A
1A
n laczacego
oczatek z koncen
Zrobilem taki rysunek i tak
A
1A
2+A
2A
3>A
1A
3
A
3A
4+A
4A
5>A
3A
5
A
5A
6+A
6A
7>A
5A
7
A
7A
8+A
8A
1>A
7A
1
Teraz co z tym zrobic bo pewnie trzeba bedzie jako to dodac ale nie wiem jak
20 sty 13:57
Ada: Ale to chyba ma być dowód ogólny.
Nie wiem czy sprytniejszą rzeczą nie byłoby zastosowanie tu indukcji matematycznej (liczba
odcinków jest liczbą naturalną tutaj).
20 sty 14:00
5-latek: czy to napisac ze
A1A2+A2A3+A3A4+A4A5+A5A6+A6A7+A7A8>A1A3+A3A5+A5A7+A7A1nie pisalem ≥ bo
rowne by byly gdyby te punkty byly wspoliniowe , a tak nie jest
20 sty 14:02
5-latek: Ada nie
To klasa 1LO .
20 sty 14:03
Ada:
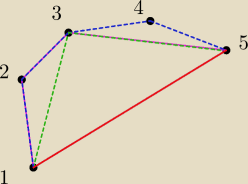
Z własności trójkątów:
13+35>15
Kiedy nad odcinkiem 13 nadbuduję trójkąt, to z tej samej własności zawsze będzie:
12+23>13
Im więcej tych trójkątów nadbuduję tym dłuższa będzie droga.
Czyli najkrótszą drogą między punktami musi być droga krótsza niż zbudowana z dwóch łamanych,
czyli w tym wypadku 15.
Nie wydaje mi się, żeby uzasadnianie tego inaczej (po za formalnym zapisem indukcyjnym), było
lepszym rozwiązaniem
20 sty 14:26
5-latek: OK
dzieki bardzo
20 sty 14:28
Ada:
20 sty 14:28