Ekstrema funkcji Klaudia: Czy funkcja y=√x²−16 ma ekstrema ?, bo mi wyszło, że nie

J: ma...

J: ..sorry ..nie ma ..

Klaudia: Dzięki

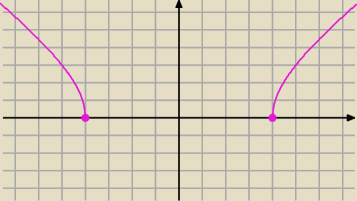
Gray: Ma; w x₀=−4 oraz x₁=4.

john2: Gray, to będą ekstrema globalne niewłaściwe?

Gray: Zależy jak zdefiniujesz takie ekstremum. Dla mnie jest to minimum globalne (więc i lokalne) właściwe − w każdym sąsiedztwie tych punktów funkcja przyjmuje wartości większe od wartości jakie osiąga w tych punktach. To, że otoczenia (sąsiedztwa) są jednostronne nie ma znaczenia.

Janek191: Wg mnie, to nie są ekstrema, lecz najmniejsza wartość funkcji y_min = 0

john2: Czyli można powiedzieć, że funkcja f(x) = √x ma minimum globalne i też lokalne w punkcie x₀ = 0 ? Ja patrzę na definicję ekstremum globalnego z wikipedii (choć może nie powinienem). Ja ją tak rozumiem, że jak np. minimum "nie powtarza się" (tzn. jego wartość nie powtarza się w innym punkcie), jak w przypadku tej funkcji Klaudii to robi, to wtedy funkcja ma właściwe.

J: ..umówmy się Panowie ... są to tzw ekstrema lokalne niewłaściwe..

john2: Ja myślałem już rok temu, że temat ekstremów mam opanowany , ale widzę, że temat nie jest jednak taki oczywisty.

Gray: Drodzy Koledzy. Najpierw dla wszystkich Nie ma swobody w interpretacji czym jest ekstremum lokalne właściwe (niewłaściwe), a czym nie jest. Definicje są precyzyjne (jak wszystko w matematyce) i wynika z nich (również z tych z nieszczęsnej wiki...), że ekstrema właściwe od niewłaściwych odróżnia nierówność ">" i "≥". W szczególności, funkcja stała to jedno wielkie ekstremum lokalne niewłaściwe, a właściwego nie ma żadnego. Niewłaściwość ekstremum nie polega na tym, że jest ono osiągane na brzegu (tj. "z drugiej strony" funkcji nie ma). Można sobie te ekstrema lokalne nazywać czasami globalnymi (o ile spełniają dodatkowe warunki), lub wartościami największymi (najmniejszymi), ale to, w myśl definicji, są jednocześnie ekstrema lokalne. Np. funkcja f:A→R ma w punkcie x₀∊A minimum lokalne, jeżeli istnieje sąsiedztwo D⊂A punktu x₀ takie, że dla x∊D: f(x)≥f(x₀). Minimum to będzie właściwe jeżeli, nierówność ≥ zastąpimy nierównością >. Funkcja sin ma np. nieskończenie wiele ekstremów lokalnych właściwych (odpowiadające 1 to maksima lokalne właściwe (i jednocześnie maksima globalne); −1 odpowiadają minima). Sprawa jest na prawdę bardzo prosta. A na zakończenie jeszcze jedno

john2: Dziękuję za piwo, ale dalej się gubię. Bo ja mam dwie wątpliwości. Według wikipedii http://pl.wikipedia.org/wiki/Ekstremum tam gdzie f(x) = cosx ma ekstrema lokalne właściwe, ma również ekstrema globalne niewłaściwe, bo wartość np. maksymalna, czyli 1, powtarza się w całej dziedzinie co 2π (czyli o tym mówi to całe jeśli dobrze rozumiem, ≥ zamiast >). Lokalne się nie powtarzają w swoich otoczeniach, dlatego są właściwe. Tak samo w przypadku funkcji Klaudii. Minimum wydaje się być w dwóch miejscach w całej dziedzinie, i ma tę samą wartość 0. Więc analogicznie powinno to być minimum globalne niewłaściwe. Są to również minima lokalne właściwe, choć to dla mnie, przyznam, nowość. I to się sprowadza do drugiego pytania. Czyli funkcja f(x) = √x Ma w punkcie (0,0) minimum lokalne właściwe (i minimum globalne właściwe)? Bo gdzieś, chyba w e−trapezie, słyszałem, że nie można mówić o ekstremum lokalnym, jeśli po jednej ze stron punktu, funkcja nie jest określona.

Gray: Ja, żeby nie mieszać dodatkowo, o maksimach globalnych właściwych i niewłaściwych nie pisałem. Funkcja √x ma maksimum lokalne (właściwe), jest to jednocześnie maksimum globalne (właściwe). Nie ma co powoływać się na jakieś tam e−trapezy; rozpisz sobie definicję i zobacz co i jak (a jeżeli masz wątpliwości − to jej zaprzeczenie: np. funkcja nie ma w punkcie x₀ minimum lokalnego właściwego, jeżeli w każdym sąsiedztwie punktu x₀ znajdziesz punkt x, taki że f(x)≤f(x₀)).

john2: Gray, dziękuję za wyjaśnienie.