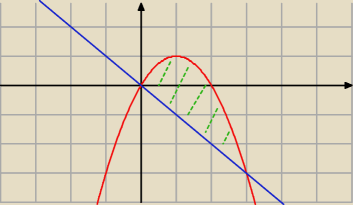
 Obliczyć pole obszaru ograniczonego krzywymi:
y = 2x−x2 x+y=0 ⇒ y = −x
−x = 2x−x2
0=3x−x2
x = 0 ∨ x = −3
Obie funkcje przesuwam o wektor v = (0,3), żeby figura leżała na osią OX. Nie zmienia to
pola obszaru.
x∊[0,3]
y∊[−x+3, −x2+2x+3]
P = ∫03 dx ∫−x+3−x2+2x+3 dy = ∫03 [y]−x+3−x2+2x+3 dx =
Obliczyć pole obszaru ograniczonego krzywymi:
y = 2x−x2 x+y=0 ⇒ y = −x
−x = 2x−x2
0=3x−x2
x = 0 ∨ x = −3
Obie funkcje przesuwam o wektor v = (0,3), żeby figura leżała na osią OX. Nie zmienia to
pola obszaru.
x∊[0,3]
y∊[−x+3, −x2+2x+3]
P = ∫03 dx ∫−x+3−x2+2x+3 dy = ∫03 [y]−x+3−x2+2x+3 dx =
| −1 | 3 | |||
= ∫03 −x2+2x+3 +x−3 dx = ∫03 −x2 +3x dx = [ | x3+ | x2] 03 = | ||
| 3 | 2 |
| −27 | 27 | 27 | −18+27 | 9 | ||||||
= | + | = −9+ | = | = | ||||||
| 3 | 2 | 2 | 2 | 2 |