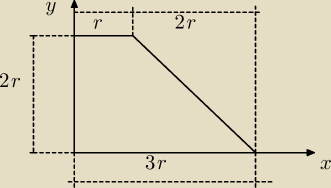
Środek ciężkości. Ryuka: Witam, czy mógłby ktoś wyznaczyć środek ciężkości tego trapezu oraz podać jego współrzędne ?

Ryuka: ?

nik:

an:

	13		5
O=(		,		)
	12		6

Min. Edukacji: http://www.obliczeniowo.com.pl/97

an: Załączyłem rysunek, ale go niema ? Dowód można znaleźć w Internecie. Dla trapezu jest to punkt przecięcia prostych: 1.Przechodząca przez środki podstaw 2x +y=3 2.Przechodząca przez punkty powstałe po przedłużeniu podstawy górnej o długość dolnej oraz dolnej o górną. 2x+7y=8

: Zawsze można sobie podzielić daną figurę na elementy o znanych osiach symetrii czyli tutaj na prostokąt i trójkąt

	r
Środek masy prostokąta lezy na przecięciu przekątnych (osi symetrii) czyli S1 (		;r),
	2

	5r		2r
natomiast trójkąta S2(		;		)
	3		3

przyjmując, że bryła(figura płaska) jest jednorodna obliczamy masy poszczególnych elementów (A−pole powierzchni figury płaskiej): masa prostokąta: m₁=ρA₁ = ρ*2r²

	1
masa trójkąta: m2 =		ρ*A2 = ρ*2r2
	2

i dalej prosto , wystarczy podstawić do wzoru na współrz. śr. masy:

	r1*m1+r2*m2+...
r→=
	m1+m2+...

czyli współrzędna iksowa:

	r   5   m1+ m2 2   3		A−1   5   ρr( + A2)   2   3		13
xśm=		=		=..=		r
	m1+m2		ρ(A1+A2)		12

daras: podobnie wyznaczamy współrzędną igrekową:

	2   r*m1+ r*m2   3		2   ρr(A1+ A2)   3
yśr.m =		=		=
	m1+m2		ρ(A1+A2)

	4r2   r(2r2+ )   3		10		5
		=		r=		r
	4r2		12		6

wredulus_pospolitus: Ale zdajecie sobie sprawę że zadanie jest sprzed 8 lat

daras: w tych zabawach wykorzystujemy 3 twierdzenia: 1. Jeżeli figura ma oś symetrii, to środek ciężkości leży na tej osi. 2. Jeżeli figura ma dwie osie symetrii, to środek ciężkości leży na ich przecięciu. 3. Jeżeli figura ma środek symetrii, to jest on jednocześnie jej środkiem ciężkości. Jeszcze jedna uwaga: zamiast określenia "środek masy" powinniśmy używać środek ciężkości wszak jesteśmy na Ziemi i to ona przyciąga każdy element bryły zatem szukając punktu jej podparcia, tak aby się nie obracała (wypadkowa momentów siły ciężkości działających na poszczególne elementy bryły = 0) znajdujemy środek ciężkości, który nie będzie się pokrywał ze środkiem masy zwłaszcza, gdy bryła jest rozciągła.

daras: @wredoto tak ale nie zostało ono do tej pory rozwiązane