kombinatoryka i rachunek prawdopodobienstwa tosia: Przy okraglym stole posadzono 4 osoby , wsrod nich sa osoby A i B. Oblicz prawdopodoboniestwa zdarzenia, ze: a) osoby A i B usiada obok siebie b) osoby A i B usiada na przeciwko siebie

Frost: Ω=4!=24 A− osoby A i B siedzą obok siebie A= 2*2!

	1
P(A)=
	6

B=2!

	1
P(B)=
	12

Zależy czy w zadaniu jest napisane, jak traktujemy sąsiadów i ustawienia. W sensie: Jeżeli osoba A ma po lewej stronie C a po prawej D a w drugim ustawieniu osoba A ma po lewej D a po prawej C. Czy takie ustawienie jest liczone raz czy 2. Sprawdź odpowiedzi i powiedz czy się zgadzają

tosia: odp. a) 2/3 b) 1/3

tosia: nie ogarniam nigdy tych stołów, pomocy

Frost: Czyli musisz moje obliczenia w A i B pomnożyć przez 4. Para A i B może się przemieszczać

tosia: mozesz mi pokazac jak to poprawnie zapisac od poczatku? chodzi mi o b), bo nie pomnoże sobie nagle na koncu *4

Frost: A=2*4*2! B=4*2!

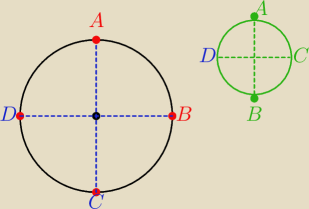
Mila: a)A− osoby A i B usiada obok siebie Obrót o 90 ^o nie zmienia układu sąsiadów.

4!
	=3!=6 na tyle sposobów mogą się ustawić 4 osoby przy okrągłym stole , za dwa różne
4

ustawienia uznajemy takie, gdy zmieniają się sąsiedzi . AB − obok siebie, mogą zmienic miejsce na 2 sposoby. (AB) traktujemy jako jeden element, to mamy 3 elementy do ustawienia.

2*3!		2*2*3
	=		=4
3		3

	4		2
P(A) =		=
	6		3

b) B− A i B usiądą naprzeciw siebie. (AB) −traktujemy jako jeden element

3!
	=2− na tyle sposobów mogą się ustawić
3

	2		1
P(B)=		=
	6		3

Tę sytuację możesz przećwiczyc w domu, bierzesz pod uwagę sąsiadów po lewej i prawej ręce.

Mila: