 Gdzie popełniłem błąd
Gdzie popełniłem błąd  Dla jakiej wartości parametru p funkcja f(x)=|x+2|+|1−x| ma dokładnie 2 rozwiązania jeśli
f(x)=p
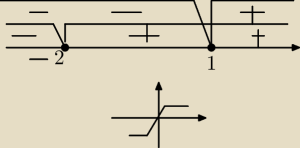
1) Wyznaczyłem miejsca zerowe modułów
x=−2, x=−2
2)
f(x)=−3 dla x∊(−∞;−2)
f(x)=2x+1 dla x∊<−2;−1)
f(x)=3 dla x∊(1;∞)
Funkcja wyszła mi tak jak na powyższym rysunku
Dla jakiej wartości parametru p funkcja f(x)=|x+2|+|1−x| ma dokładnie 2 rozwiązania jeśli
f(x)=p
1) Wyznaczyłem miejsca zerowe modułów
x=−2, x=−2
2)
f(x)=−3 dla x∊(−∞;−2)
f(x)=2x+1 dla x∊<−2;−1)
f(x)=3 dla x∊(1;∞)
Funkcja wyszła mi tak jak na powyższym rysunku
 |1−x|=|x−1|
f(x)=|x+2|+|x−1|
1) |x+2|=x+2 dla x≥−2
2) |x−1|=x−1 dla x≥1
a) x<−2
f(x)=−x−2−x+1=−2x−1
b) x∊<−2,1)
f(x)=x+2−x+1=3
c) x≥1
f(x)=x+2+x−1
f(x)=2x+1
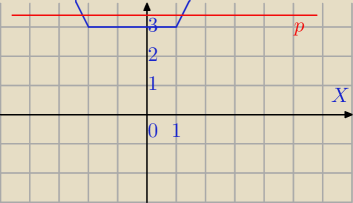
f(x)=p Dwa rozwiązania dla p>3
|1−x|=|x−1|
f(x)=|x+2|+|x−1|
1) |x+2|=x+2 dla x≥−2
2) |x−1|=x−1 dla x≥1
a) x<−2
f(x)=−x−2−x+1=−2x−1
b) x∊<−2,1)
f(x)=x+2−x+1=3
c) x≥1
f(x)=x+2+x−1
f(x)=2x+1
f(x)=p Dwa rozwiązania dla p>3