 Najdłuższy bok AB trojkata ABC ma długość √218 oraz wektor CB=[10, −10] i CA=[−3, −3]. Wykaz
ze pole kola opisanego na tym trojkącie wynosi 54,5π.
Z góry dziękuje za pomoc
Najdłuższy bok AB trojkata ABC ma długość √218 oraz wektor CB=[10, −10] i CA=[−3, −3]. Wykaz
ze pole kola opisanego na tym trojkącie wynosi 54,5π.
Z góry dziękuje za pomoc

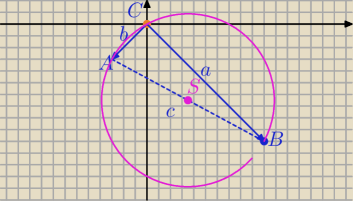 b=3√2
a=10√2
c=√218
c2=218
a2+b2=9*2+100*2=218⇔
ΔABC jest trójkątem prostokątnym.
b=3√2
a=10√2
c=√218
c2=218
a2+b2=9*2+100*2=218⇔
ΔABC jest trójkątem prostokątnym.
| 1 | 1 | |||
R= | |AB|= | √218 | ||
| 2 | 2 |
| 1 | 218π | |||
Pkoła=π*( | √218)2= | =54.5π | ||
| 2 | 4 |


