 A) 3x2−x<0
B) x2−3≥0
A) 3x2−x<0
B) x2−3≥0
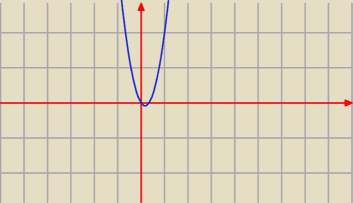 a) 3x2−x<0
x(3x−1)<0
Okreslam teraz miejsca zerowe
a) 3x2−x<0
x(3x−1)<0
Okreslam teraz miejsca zerowe
| 1 | ||
x=0 lub 3x−1=0 to 3x=1 to x= | ||
| 3 |
| 1 | ||
Teraz to musi byc <0 to musi lezec pod osia OX wiec widziesz ze x nalezy (0, | ) | |
| 3 |
 b) x2−3≥0 Widzisz wzor skroconego mnozenia a2−b2=(a+b)(a−b) wiec x2−3≥0
(x−√3)(x+√3)≥0 wylicz xsy z tych nawiasow (to beda m miejsca zerowe
Wykres tej funkcji czyli y=x2−3 wyglada tak
Na czarno masz zaznaczone wyliczone miejsca zerowe ktore tez naleza do rozwiazania nierownowsci
bo masz nieroownosc slaba . Widzisz juz przedzialy gdzie ta nierownosc jest ≥0
b) x2−3≥0 Widzisz wzor skroconego mnozenia a2−b2=(a+b)(a−b) wiec x2−3≥0
(x−√3)(x+√3)≥0 wylicz xsy z tych nawiasow (to beda m miejsca zerowe
Wykres tej funkcji czyli y=x2−3 wyglada tak
Na czarno masz zaznaczone wyliczone miejsca zerowe ktore tez naleza do rozwiazania nierownowsci
bo masz nieroownosc slaba . Widzisz juz przedzialy gdzie ta nierownosc jest ≥0
