zadanie
Blue: | | | |
Wyznacz, które liczby spełniające nierówność | ≤n są jednocześnie pierwiastkami |
| | |
wielomianu W(x)= (x
4−16)(x
2−16)
2.
Mi wyszło, że 4,2,−2,−4.... ale w odpowiedzi mam tylko 4....
Dlaczego?
18 sty 23:37
Eta:
n∊N i n≥3
18 sty 23:39
Blue: No tak, założenia... wiedziałam, że o czymś musiałam zapomnieć, dzięki

18 sty 23:58
pigor: ..., tu może np. tak :
| | | | | |
≤ n ⇔ | ≤ n ⇔ | ≤ n i (*) n ≥3 ⇒ |
| | | |
| | n(n−1)(n−2) | |
⇒ |
| ≤ n ⇔ (n−1)(n−2) ≤ 6 ⇔ n2−3n−4 ≤ 0 ⇔ |
| | 3*2*1 | |
⇔
(n+1)(n−4) ≤ 0 , stąd i z (*) 3 ≤ n ≤ 4 ⇔
n∊{3, 4} stąd
i z postaci wielomianu W wynika, że tylko
n=4 jest jednocześnie
tego wielomianu pierwiastkiem . ...

19 sty 01:09
Blue: Pigor już rozumiem, po prostu zapomniałam o założeniu

19 sty 16:58
tosia: Droga Blue skąd bierzesz takie ciekawe zadania mogłabyś powiedzieć z jakich zbiorów korzystasz
pozdrawiam
19 sty 21:47
19 sty 21:57
Gość: Mógłby ktoś wyjaśnić, dlaczego z tego dwumianu, wychodzi nam n∊{3,4}?
30 gru 23:05
wredulus_pospolitus:
nie bardzo rozumiem co nie jest jasne w rozwiązaniu tej nierówności przez pigor'a
30 gru 23:24
Gość: Tak, jak sam doszedłem do (n+1)(n−4)≤0, to nie rozumiem tej części "stąd i z (*) 3 ≤ n ≤ 4"
30 gru 23:41
gostek:
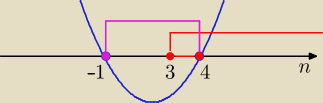
30 gru 23:48
wredulus_pospolitus:
| | | | | |
ewentualnie: | = | −−−> n ≥ 3 |
| | | |
przeciwnym razie dwumian Newtona 'nie ma sensu'.
30 gru 23:50
Gość: Już wszystko jasne, dzięki

31 gru 00:03




